【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把P1(y1,x1)叫做点P的友好点,已知点A1的友好点为A2,点A2的友好点为A3,点A3的友好点为A4,,这样依次得到各点.若A2020的坐标为(3,2),设A1(x,y),则xy的值是( )
A.-5B.-1C.3D.5
参考答案:
【答案】C
【解析】
列出部分An点的坐标,根据坐标的变化寻找规律,规律和A2020的坐标结合起来,即可得出答案.
解:∵设A1(x,y),
∴A2(y-1,-x-1),
∴A3(-x-1-1,-y+1-1),
即A3(-x-2,-y),
∴A4(-y-1,x+2-1),
即A4(-y-1,x+1),
∴A5(x+1-1,y+1-1),
即A5(x,y)与A1相同,
可以观察到友好点是4个一组循环的,
∵2020÷4=505,
∴A2020(3,2)与A4是相同的,
![]() ,
,
解得![]() ,
,
∴x+y=1+2=3;
故答案为:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路去上学,她先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中的折线ABCDE表示小丽和学校之间的距离y(米)与她离家的时间x(分)之间的函数关系.
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,先填好下表,再写出总运费y关于x的函数关系式;

(2)若要求总运费不超过900元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点E,F分别在AB,CD上,AF⊥CE,垂足为点O,∠1=∠B,
∠A+∠2=90°.求证:AB∥CD.
证明:如图,
∵∠1=∠B(已知)
∴CE∥BF(同位角相等,两直线平行)
______________
∴∠AFC+∠2=90°(等式性质)
∵∠A+∠2=90°(已知)
∴∠AFC=∠A(同角或等角的余角相等)
∴AB∥CD(内错角相等,两直线平行)
请你仔细观察下列序号所代表的内容:
①∴∠AOE=90°(垂直的定义)
②∴∠AFB=90°(等量代换)
③∵AF⊥CE(已知)
④∵∠AFC+∠AFB+∠2=180°(平角的定义)
⑤∴∠AOE=∠AFB(两直线平行,同位角相等)
横线处应填写的过程,顺序正确的是( )

A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校区内有甲、乙两块大小一样的长方形地块,地块长30m,宽25m,现要在长方形地块内分别修筑如图所示的两条平行四边形小路(图中阴影部分),余下的部分绿化.现已知ABCD1m,EFGH1m,记甲、乙地块的绿化面积分别为S1、S2,则S1、S2的大小关系是( )

A.S1<S2B.S1=S2C.S1>S2D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
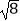 +
+ 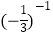 ﹣|2sin45°﹣1|.
﹣|2sin45°﹣1|.
相关试题

