【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.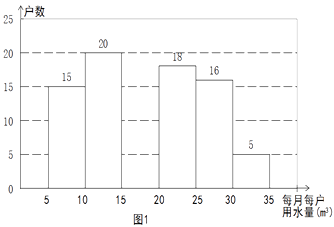

小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n = , 小明调查了户居民,并补全图1;
(2)每月每户用水量的中位数落在之间,众数落在之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
参考答案:
【答案】
(1)![]() ,
,![]() ,
,
(2)![]() ,
,![]()
(3)解:∵ ![]()
∴ ![]() (户)
(户)
答:居民户数有700户
【解析】(1) ![]() ,
, ![]() ,补图如下:
,补图如下:

( 2 ) ![]() ,
, ![]() ,
,
根据n=360°-120°-30°=210°,再根据有7户居民对用水价格调价涨幅抱无所谓,根据居民对用水价格调价涨幅抱无所谓所占的圆心角的度数求出百分比,即可求出调查的总人数。然后求出每户用水量在15-20之间的户数,即可补全统计图。
(2)根据定义,把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据。即可求解。
(3)用小区居民的总人数![]() “视调价涨幅采取相应的用水方式改变”的居民数占被调查的居民数的百分比,计算即可。
“视调价涨幅采取相应的用水方式改变”的居民数占被调查的居民数的百分比,计算即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正方形,
是正方形, 是等边三角形.
是等边三角形.(1)求证:
 ;
;(2)求
 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把长方形
 沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,
沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,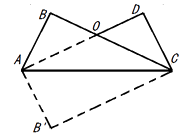
(1)求∠AOC和∠BAC的度数;
(2)若AD= ,OD=
,OD=  ,求CD的长
,求CD的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(3,-2),则点P在第_____________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-2)2的算术平方根是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC的( )
A. 三边垂直平分线的交点 B. 三条内角平分线的交点
C. 三条高的交点 D. 三条中线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=-x+b的图象与正比例函数y=kx的图象都经过点B(3,1)
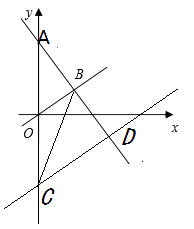
(1)求一次函数和正比例函数的表达式;
(2)若直线CD与正比例函数y=kx平行,且过点C(0,-4),与直线AB相交于点D,求点D的坐标.(注:二直线平行,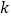 相等)
相等)
(3)连接CB,求三角形BCD的面积.
相关试题

