【题目】如图,在平面直角坐标系中,一次函数y=-x+b的图象与正比例函数y=kx的图象都经过点B(3,1)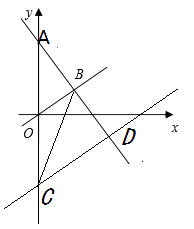
(1)求一次函数和正比例函数的表达式;
(2)若直线CD与正比例函数y=kx平行,且过点C(0,-4),与直线AB相交于点D,求点D的坐标.(注:二直线平行, ![]() 相等)
相等)
(3)连接CB,求三角形BCD的面积.
参考答案:
【答案】
(1)解:把B(3,1)分别代入y=-x+b和y=kx得
![]() ,
, ![]()
解之得: ![]() ,
, ![]()
∴ ![]() ,
, ![]()
(2)解:∵二直线平行,CD经过C(0,-4)
∴直线CD为 ![]()
由题意得: 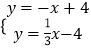
解之得 ![]()
∴点D为(6,-2)
(3)解:易得A(0,4)
∴AC=8
∴ ![]()
【解析】(1)利用待定系数法,将点B的坐标分别代入两函数解析式,建立方程求解,即可两函数解析式。
(2)根据两直线平行k值相等,就可以求出直线CD函数解析式,再将两函数解析式联立方程组,解方程组,求解即可得出交点D的坐标。
(3)先求出点A的坐标,再根据S△BCD=S△ACD-S△ABC。计算即可求出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
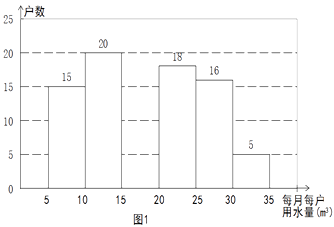

小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n = , 小明调查了户居民,并补全图1;
(2)每月每户用水量的中位数落在之间,众数落在之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(-2)2的算术平方根是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC内一点P满足PA=PB=PC,则点P一定是△ABC的( )
A. 三边垂直平分线的交点 B. 三条内角平分线的交点
C. 三条高的交点 D. 三条中线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,2)关于y轴的对称点为( )
A.(1,2)
B.(﹣1,﹣2)
C.(2,﹣1)
D.(1,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若点M(1,b)与点N(1,3)之间的距离是5,则b的值是___________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若圆锥的底面半径为3,母线长为5,则这个圆锥的侧面积为( )
A.6π
B.8π
C.15π
D.30π
相关试题

