【题目】如图,四边形![]() 是正方形,
是正方形,![]() 是等边三角形.
是等边三角形.
(1)求证:![]() ;
;
(2)求![]() 的度数.
的度数.

参考答案:
【答案】(1)证明见解析(2) 150°.
【解析】
试题分析:(1)根据正方形、等边三角形的性质,可以得到AB=BE=CE=CD,∠ABE=∠DCE=30°,由此即可证明;
(2)只要证明∠EAD=∠ADE=15°,即可解决问题;
试题解析:(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
 ,
,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,
∴∠BAE=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(x﹣3,2x+4)在x轴上,则点P的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果用有序数对(3,2)表示教室里第3列第2排的座位,则位于第5列第4排的座位应记作( )
A.(4,5)B.(5,4)C.(5,2)D.(4,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,是3x2y的同类项的是( )
A.3a2b
B.﹣2xy2
C.x2y
D.3xy -
科目: 来源: 题型:
查看答案和解析>>【题目】把长方形
 沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,
沿对角形线AC折叠,得到如图所示的图形,已知∠BAO=30°,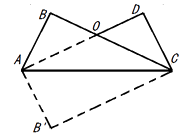
(1)求∠AOC和∠BAC的度数;
(2)若AD= ,OD=
,OD=  ,求CD的长
,求CD的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知P(3,-2),则点P在第_____________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
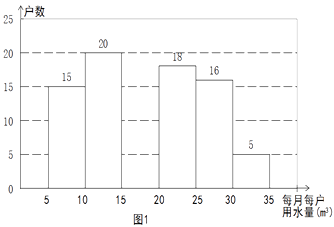

小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n = , 小明调查了户居民,并补全图1;
(2)每月每户用水量的中位数落在之间,众数落在之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
相关试题

