【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点A,B,C都在格点(正方形网格的交点称为格点).现将△ABC平移,使点A平移到点D,点E、F分别是B、C的对应点.
(1)在图中请画出平移后的△DEF,并求出△DFF的面积;
(2)在网格中找格点P,使S△ABC=S△BCP,这样的格点P有多少个.

参考答案:
【答案】(1)7;(2)4.
【解析】
(1)依据平移的性质,即可得到△DEF,利用割补法即可得到△DFF的面积;(2)过A作BC的平行线,过E作BC的平行线,即可得出格点P有4个.
(1)如图所示,△DEF即为所求,△DFF的面积=4×4﹣![]() ×2×4﹣
×2×4﹣![]() ×1×4﹣
×1×4﹣![]() ×2×3=7;
×2×3=7;

(2)如图,过A作BC的平行线,过E作BC的平行线,
当点P在点P1,点P2,点P3,点P4处时,存在S△ABC=S△BCP,
∴格点P有4个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2,……第n次平移将长方形An﹣1Bn﹣1 Cn﹣1 Dn﹣1 的方向平移6个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为2018,则n的值为( )

A. 334 B. 335 C. 336 D. 337
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小颖在教学楼四层楼上,每层楼高均为3米,测得目高1.5米,看到校园里的圆形花园最近点的俯角为60°,最远点的俯角为30°,请你帮小颖算出圆形花园的面积是多少平方米?(结果保留1位小数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线PQ∥MN,点A在PQ上,直角△BEF的直角边BE在MN上,且∠B=90°,∠BEF=30°.现将△BEF绕点B以每秒1°的速度按逆时针方向旋转(E,F的对应点分别是E′,F′),同时,射线AQ绕点A以每秒4°的速度按顺时针方向旋转(Q的对应点是Q′).设旋转时间为t秒(0≤t≤45).
(1)∠MBF′=__.(用含t的代数式表示)
(2)在旋转的过程中,若射线AQ′与边E′F′平行时,则t的值为__.

-
科目: 来源: 题型:
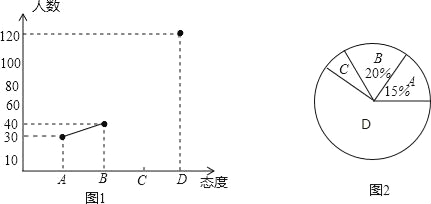
查看答案和解析>>【题目】中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了市区某校七年级若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).统计员在将测试数据绘制成图表时发现,反对漏统计6人,赞成漏统计4人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
家长对中学生带手机上学各项态度人数统计表和统计图:
态度
调整前人数
调整后人数
A.无所谓
30
30
B.基本赞成
40
40
C.赞成
D.反对
114
120
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)填写统计表,并根据调整后数据补全折线统计图;
(3)根据抽样调查结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价为120元、170元的A,B两种型号的电风扇,如表所示是近2周的销售情况:(进价、售价均保持不变,利润=销售收入一进货成本)
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
6
5
2200元
第二周
4
10
3200元
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市再采购这两种型号的电风扇共130台,并且全部销售完,该超市能否实现这两批的总利润为8010元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
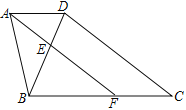
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线分别交BD、BC于点E、F,且AE∥CD
(1) 求AD的长;
(2) 若∠C=30°,求CD的长.
相关试题

