搜索
【题目】如图，一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，则函数y=ax2+（b﹣1）x+c的图象可能是（ ）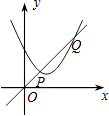
A.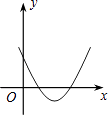
B.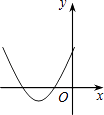
C.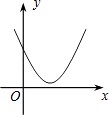
D.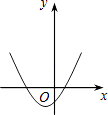
参考答案：
【答案】A
【解析】解：∵一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，
∴方程ax2+（b﹣1）x+c=0有两个不相等的根，
∴函数y=ax2+（b﹣1）x+c与x轴有两个交点，
又∵﹣ 
＞0，a＞0
∴﹣ 
=﹣ + 
＞0
∴函数y=ax2+（b﹣1）x+c的对称轴x=﹣ ＞0，
∴A符合条件，
故选A．
由一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点，得出方程ax2+（b﹣1）x+c=0有两个不相等的根，进而得出函数y=ax2+（b﹣1）x+c与x轴有两个交点，根据方程根与系数的关系得出函数y=ax2+（b﹣1）x+c的对称轴x=﹣ ＞0，即可进行判断．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a、b、c满足|a﹣
|+
+（c﹣4
）2=0．（1）求a、b、c的值；
（2）判断以a、b、c为边能否构成三角形？若能构成三角形，此三角形是什么形状？并求出三角形的面积；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了激发学生爱数学、学数学、用数学的热情，某学校在七年级开展“魅力数学”趣味竞赛，该校七年级共有学生400人参加竞赛．现随机抽取40名参赛学生的成绩数据（百分制）进行整理、描述和分析．
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范围
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
频数
1
m
13
9
14
平均数、中位数、众数如下表所示：
平均数
中位数
众数
84.1
n
89
根据以上信息，回答下列问题：
（1）m＝ ，n＝ ；
（2）小明说：“这次竞赛我得了84分，在所有参赛学生中排名属中等偏上!”小明的说法 （填“正确”或“不正确”），理由是 ；
（3）若成绩不低于85分可以进入决赛，估计参赛的400名学生中能进入决赛的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y=
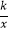（x＞0）的图象与一次函数y=3x的图象相交于点A，其横坐标为2．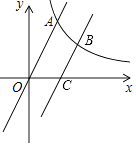
（1）求k的值；
（2）点B为此反比例函数图象上一点，其纵坐标为3．过点B作CB∥OA，交x轴于点C，直接写出线段OC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ACB=90°，AC =3，BC =4，AB=5，BD平分∠ABC，如果M、N分别为BD、BC上的动点，那么CM+MN的最小值是____．
-
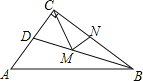
科目： 来源： 题型：
查看答案和解析>>【题目】某学校为了丰富学生的大课间活动，准备购进一批跳绳，已知2根短绳和1根长绳共需56元，1根短绳和2根长绳共需82元．
（1）求每根短绳和每根长绳的售价各是多少元？
（2）学校准备购进这两种跳绳共50根，并且短绳的数量不超过长绳数量的2倍，总费用不超过1020元，请设计出最省钱的购买方案，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】假设我市出租车收费标准是：起步价6元，可乘3千米；3千米到5千米，每千米1.6元；超过5千米，每千米2.4元.
（1）若某人乘坐的路程为4千米，那么他支付的费用是多少？
（2）若某人乘坐了x(x＞5)千米的路程，则他应支付的费用是多少？
（3）若某人乘坐的路程为10千米，那么他应支付的费用是多少？
相关试题
