【题目】某学校为了丰富学生的大课间活动,准备购进一批跳绳,已知2根短绳和1根长绳共需56元,1根短绳和2根长绳共需82元.
(1)求每根短绳和每根长绳的售价各是多少元?
(2)学校准备购进这两种跳绳共50根,并且短绳的数量不超过长绳数量的2倍,总费用不超过1020元,请设计出最省钱的购买方案,并说明理由.
参考答案:
【答案】(1)每根短绳售价是10元,每根长绳的售价是36元;(2)当购买短绳33根,长绳17根时,最省钱.
【解析】
(1)设每根短绳售价是x元,每根 长绳的售价是y元,根据:“2根短绳和1根长绳共需56元,1根短绳和2根长绳共需82元”列方程组求解即可;
(2)首先根据“短绳的数量不多于长绳数量的2倍”确定自变量的取值范围,然后得到有关总费用和短绳之间的关系得到函数解析式,确定函数的最值即可.
解:(1)设每根短绳售价是x元,每根长绳的售价是y元,
根据题意,得![]() ,
,
解得:![]() ,
,
答:每根短绳售价是10元,每根长绳的售价是36元;
(2)设购进短绳m根,总费用为W元,
根据题意,得:W=10m+36(50-m)=-26m+1800,
∵-26<0,
∴W随m的增大而减小,
又∵m≤2(50-m),解得:m≤![]() ,
,
而m为正整数,
∴当m=33时,W最小=-26×33+1800=942,
942<1020,符合题意,
此时50-33=17,
答:当购买短绳33根,长绳17根时,最省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
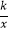 (x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.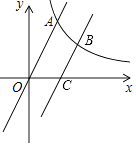
(1)求k的值;
(2)点B为此反比例函数图象上一点,其纵坐标为3.过点B作CB∥OA,交x轴于点C,直接写出线段OC的长. -
科目: 来源: 题型:
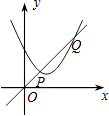
查看答案和解析>>【题目】如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )
A.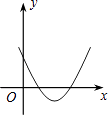
B.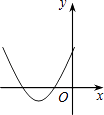
C.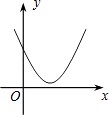
D.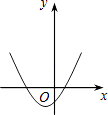
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
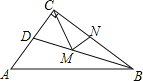
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设我市出租车收费标准是:起步价6元,可乘3千米;3千米到5千米,每千米1.6元;超过5千米,每千米2.4元.
(1)若某人乘坐的路程为4千米,那么他支付的费用是多少?
(2)若某人乘坐了x(x>5)千米的路程,则他应支付的费用是多少?
(3)若某人乘坐的路程为10千米,那么他应支付的费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)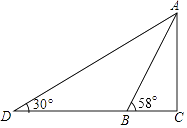
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由6个正方形拼成的一个长方形,如果最小的正方形的边长为1
(Ⅰ)能否求出拼成的长方形的面积?____(填“能”或“不能”);
(Ⅱ)若能,请你写出拼成的长方形的面积;若不能,请说明理由.

相关试题

