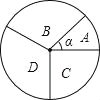
【题目】我市为了解中学生的视力情况,对某校三个年级的学生视力进行了抽样调查,得到不完整的统计表与扇形统计图如下,其中扇形统计图的圆心角α为36°,x表示视力情况,根据上面提供的信息,回答下列问题:
分组 | 视力情况 | 频数 | 频率 |
A | 4.0≤x<4.3 | 20 | |
B | 4.3≤x<4.6 | 0.35 | |
C | 4.6≤x<4.9 | 50 | |
D | x≥4.9 |
(1)此次共调查了 人;
(2)请将表格补充完整;
(3)这组数据的中位数落在 组内;
(4)扇形统计图中“D组”的扇形所对的圆心角的度数是 .
参考答案:
【答案】(1)200;(2)补图见解析;(3)C;(4)108°.
【解析】
试题分析:(1)根据圆心角α为36°,求出A组所占的百分比,的出频率,再根据频数是20,即可得出总人数;
(2)根据频数、频率之间的关系,分别求出B组的频数、C组的频率、D组的频数以及频率,填表即可;
(3)根据中位数的定义即可得出这组数据的中位数落在C组内;
(4)用360°乘以D组的频率即可得出答案.
试题解析:(1)∵圆心角α为36°,
∴A组的频率是:![]() =0.1,
=0.1,
∴总人数是20÷0.1=200(人),
(2)B组的频数是200×0.35=70;
C组的频率是50÷200=0.25;
D组的频数是:200-20-70-50=60,
频率是60÷200=0.3;
填表如下:
分组 | 视力情况 | 频数 | 频率 |
A | 4.0≤x<4.3 | 20 | 0.1 |
B | 4.3≤x<4.6 | 70 | 0.35 |
C | 4.6≤x<4.9 | 50 | 0.25 |
D | x≥4.9 | 60 | 0.30 |
(3)∵这组数据共有200个数,
∴中位数是第100,101个数的平均数,
∴这组数据的中位数落在C组内;
(4)扇形统计图中“D组”的扇形所对的圆心角的度数是360°×0.30=108°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=-
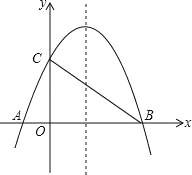
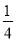 x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴方程;
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果正确的是( )
A.(x2)3=x5
B.3x2+2x2=5x4
C.x3x3=x6
D.(x+y)2=x2+y2 -
科目: 来源: 题型:
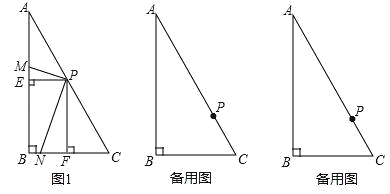
查看答案和解析>>【题目】已知:在Rt△ABC中,∠ABC=90°,∠C=60°,现将一个足够大的直角三角形的顶点P放在斜边AC上.
(1)设三角板的两直角边分别交边AB,BC于点M,N.
①当点P是AC的中点时,分别作PE⊥AB于点E,PF⊥BC于点F,得到图1,写出图中的一对全等三角形;
②在①的条件下,写出与△PEM相似的三角形,并直接写出PN与PM的数量关系.
(2)移动点P,使AP=2CP,将三角板绕点P旋转,设旋转过程中三角板的两直角边分别交边AB,BC于点M,N(PM不与边AB垂直,PN不与边BC垂直);或者三角板的两直角边分别交边AB,BC的延长线于点M,N.
①请在备用图中画出图形,判断PM与PN的数量关系,并选择其中一种图形证明你的结论;
②在①的条件下,当△PCN是等腰三角形时,若BC=3cm,则线段BN的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】围棋有黑、白两种棋子,混合在一起后,随意从中摸出3个棋子,正好颜色相同,这是事件(填“必然”、“不可能”或“不确定”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:“△ABC中至少有两个锐角”,第一步假设为____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点 A 2, 1 向左平移 3 个单位长度,再向上平移 4 个单位长度得到点 B ,则点 B 的坐标是( )
A. 5, 3B. 1, 3C. 1, 5D. 5, 5
相关试题

