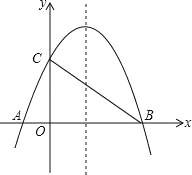
【题目】如图,已知抛物线y=-![]() x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
(1)求抛物线的解析式及其对称轴方程;
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
参考答案:
【答案】(1) y=-![]() x2+
x2+![]() x+4,x=3;(2)△AOC∽△COB.(3)4;(4)点Q的坐标为(3,4+
x+4,x=3;(2)△AOC∽△COB.(3)4;(4)点Q的坐标为(3,4+![]() )或(3,4-
)或(3,4-![]() )或(3,0)时,△ACQ为等腰三角形时.
)或(3,0)时,△ACQ为等腰三角形时.
【解析】
试题分析:(1)把点B的坐标代入抛物线解析式求出b的值,即可得到抛物线解析式,再根据对称轴方程列式计算即可得解;
(2)令y=0,解方程求出点A的坐标,令x=0求出y的值得到点C的坐标,再求出OA、OB、OC,然后根据对应边成比例,夹角相等的两个三角形相似证明;
(3)设直线BC的解析式为y=kx+b,利用待定系数法求出解析式,再表示出MN,然后根据二次函数的最值问题解答;
(4)利用勾股定理列式求出AC,过点C作CD⊥对称轴于D,然后分①AC=CQ时,利用勾股定理列式求出DQ,分点Q在点D的上方和下方两种情况求出点Q到x轴的距离,再写出点的坐标即可;②点Q为对称轴与x轴的交点时,AQ=CQ,再写出点Q的坐标即可.
试题解析:(1)∵点B(8,0)在抛物线y=-![]() x2+bx+4上,
x2+bx+4上,
∴-![]() ×64+8b+4=0,
×64+8b+4=0,
解得b=![]() ,
,
∴抛物线的解析式为y=-![]() x2+
x2+![]() x+4,
x+4,
对称轴为直线x=-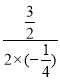 =3;
=3;
(2)△AOC∽△COB.
理由如下:令y=0,则-![]() x2+
x2+![]() x+4=0,
x+4=0,
即x2-6x-16=0,
解得x1=-2,x2=8,
∴点A的坐标为(-2,0),
令x=0,则y=4,
∴点C的坐标为(0,4),
∴OA=2,OB=8,OC=4,
∵![]() =2,∠AOC=∠COB=90°,
=2,∠AOC=∠COB=90°,
∴△AOC∽△COB;
(3)设直线BC的解析式为y=kx+b,
则![]() ,
,
解得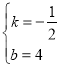 ,
,
∴直线BC的解析式为y=-![]() x+4,
x+4,
∵MN∥y轴,
∴MN=-![]() x2+
x2+![]() x+4-(-
x+4-(-![]() x+4),
x+4),
=-![]() x2+
x2+![]() x+4+
x+4+![]() x-4,
x-4,
=-![]() x2+2x,
x2+2x,
=-![]() (x-4)2+4,
(x-4)2+4,
∴当x=4时,MN的值最大,最大值为4;
(4)由勾股定理得,AC=![]() ,
,
过点C作CD⊥对称轴于D,则CD=3,

①AC=CQ时,DQ=![]() =
=![]() ,
,
点Q在点D的上方时,点Q到x轴的距离为4+![]() ,
,
此时点Q1(3,4+![]() ),
),
点Q在点D的下方时,点Q到x轴的距离为4-![]() ,
,
此时点Q2(3,4-![]() ),
),
②点Q为对称轴与x轴的交点时,AQ=5,
CQ=![]() =5,
=5,
∴AQ=CQ,
此时,点Q3(3,0),
③当AC=AQ时,∵AC=![]() ,点A到对称轴的距离为5,
,点A到对称轴的距离为5,![]() <5,∴这种情形不存在.
<5,∴这种情形不存在.
综上所述,点Q的坐标为(3,4+![]() )或(3,4-
)或(3,4-![]() )或(3,0)时,△ACQ为等腰三角形时.
)或(3,0)时,△ACQ为等腰三角形时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王玲和李凯进行投球比赛,每人连投12次,投中一次记2分,投空一次记1分,王玲先投,投得16分,李凯要想超过王玲,应至少投中________次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组图形中都是平面图形的是( )
A. 三角形、圆、球、圆锥 B. 点、线、面、体
C. 角、三角形、正方形、圆 D. 点、相交线、线段、长方体
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的算术平方根是( )
A. ﹣2 B. ±2 C. 2 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果正确的是( )
A.(x2)3=x5
B.3x2+2x2=5x4
C.x3x3=x6
D.(x+y)2=x2+y2 -
科目: 来源: 题型:
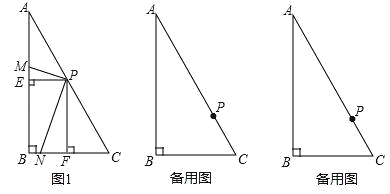
查看答案和解析>>【题目】已知:在Rt△ABC中,∠ABC=90°,∠C=60°,现将一个足够大的直角三角形的顶点P放在斜边AC上.
(1)设三角板的两直角边分别交边AB,BC于点M,N.
①当点P是AC的中点时,分别作PE⊥AB于点E,PF⊥BC于点F,得到图1,写出图中的一对全等三角形;
②在①的条件下,写出与△PEM相似的三角形,并直接写出PN与PM的数量关系.
(2)移动点P,使AP=2CP,将三角板绕点P旋转,设旋转过程中三角板的两直角边分别交边AB,BC于点M,N(PM不与边AB垂直,PN不与边BC垂直);或者三角板的两直角边分别交边AB,BC的延长线于点M,N.
①请在备用图中画出图形,判断PM与PN的数量关系,并选择其中一种图形证明你的结论;
②在①的条件下,当△PCN是等腰三角形时,若BC=3cm,则线段BN的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市为了解中学生的视力情况,对某校三个年级的学生视力进行了抽样调查,得到不完整的统计表与扇形统计图如下,其中扇形统计图的圆心角α为36°,x表示视力情况,根据上面提供的信息,回答下列问题:
分组
视力情况
频数
频率
A
4.0≤x<4.3
20
B
4.3≤x<4.6
0.35
C
4.6≤x<4.9
50
D
x≥4.9
(1)此次共调查了 人;
(2)请将表格补充完整;
(3)这组数据的中位数落在 组内;
(4)扇形统计图中“D组”的扇形所对的圆心角的度数是 .
相关试题

