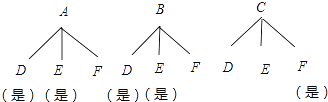
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)由乙固定在E处,移动甲后黑色方块构成的拼图一共有3种可能,其中有两种情形是轴对称图形,所以若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是![]() ;(2)①由树状图得到黑色方块所构拼图是轴对称图形的概率;②黑色方块所构拼图中是中心对称图形有两种情形,①甲在B处,乙在F处,②甲在C处,乙在E处,所以黑色方块所构拼图是中心对称图形的概率是
;(2)①由树状图得到黑色方块所构拼图是轴对称图形的概率;②黑色方块所构拼图中是中心对称图形有两种情形,①甲在B处,乙在F处,②甲在C处,乙在E处,所以黑色方块所构拼图是中心对称图形的概率是![]() .
.
(1)若乙固定在E处,移动甲后黑色方块构成的拼图一共有3种可能,其中有两种情形是轴对称图形,所以若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 ![]() .
.
故答案为![]() .(2)①由树状图可知,黑色方块所构拼图是轴对称图形的概率=
.(2)①由树状图可知,黑色方块所构拼图是轴对称图形的概率= ![]() .
.
②黑色方块所构拼图中是中心对称图形有两种情形,
甲在B处,乙在F处或甲在C处,乙在E处,
所以黑色方块所构拼图是中心对称图形的概率是 ![]() .
.
故答案为 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,若AC=3,CE=4,则AD2+BE2=__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形
 的边长为8,点
的边长为8,点 是边
是边 上一动点(不与点
上一动点(不与点 重合),以
重合),以 为边在
为边在 的下方作等边三角形
的下方作等边三角形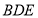 ,连接
,连接 .
.
(1)在运动的过程中,
 与
与 有何数量关系?请说明理由.
有何数量关系?请说明理由.(2)当BE=4时,求
 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学玩摸球游戏,准备了甲、乙两个口袋,其中甲口袋中放有标号为1,2,3,4,5的5个球,乙口袋中放有标号为1,2,3,4的4个球.游戏规则:甲从甲口袋摸一球,乙从乙口袋摸一球,摸出的两球所标数字之差(甲数字﹣乙数字)大于0时甲胜,小于0时乙胜,等于0时平局.你认为这个游戏规则对双方公平吗?请说明理由.若不公平,请你对本游戏设计一个对双方都公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 (
( ,
, 、
、 、
、 为常数)的图象如图所示,下列
为常数)的图象如图所示,下列 个结论:①
个结论:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ 为常数,且
为常数,且 .其中正确的结论有( )
.其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 ,
, ,
, 是常数,且
是常数,且 中的
中的 与
与 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )









 ;
; 当
当 时,
时, ;
; 当
当 时,
时, 的值随
的值随 值的增大而减小;
值的增大而减小; 方程
方程 有两个不相等的实数根.
有两个不相等的实数根.A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 与
与 轴交于点
轴交于点 ,顶点为点
,顶点为点 ,点
,点 与点
与点 关于抛物线的对称轴对称.
关于抛物线的对称轴对称.
 求直线
求直线 的解析式;
的解析式; 点
点 在抛物线上,且点
在抛物线上,且点 的横坐标为
的横坐标为 .将抛物线在点
.将抛物线在点 ,
, 之间的部分(包含点
之间的部分(包含点 ,
, )记为图象
)记为图象 ,若图象
,若图象 向下平移
向下平移 个单位后与直线
个单位后与直线 只有一个公共点,求
只有一个公共点,求 的取值范围.
的取值范围.
相关试题

