【题目】如图,在直角△ABC中,∠ACB=90°,AC=3,BC=4,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD于M,EN⊥DC于N.
(1)当AD=CD时,求证DE//AC;
(2)当∠MBE与△CNE的某一个内角相等时,求AD的长;
(3)当四边形MEND与△BDE的面积相等时,求AD的长.

参考答案:
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由等腰三角形的性质得出∠A=∠DCA,由三角形的外角性质和角平分线得出得出∠C=∠BDE,即可得出结论;(2)存在以下两种情况①当∠B=∠ECN时;②当∠B=∠CNE时,根据相似三角形的性质即可求得;(3)根据四边形MEND与△BDE的面积相等,得到△DME与△BME的面积相等.证明△BME∽△BCA,△CDE∽△CBD,即可解答.
试题解析:
(1)证明:∵AD=CD,
∴∠A=∠ACD.
∵∠CDB=∠A+∠ACD,
∴∠CDB=2∠A.
∵DE平分∠CDB,
∴∠BDE=![]() ∠CDB=∠A.
∠CDB=∠A.
∴DE∥AC.
(2)∵∠ACB=90°,AC=3,BC=4,
∴AB=5.
∵EM⊥BD,EN⊥CD,
∴∠BME=∠CNE=90°.
存在以下两种情况
①当∠B=∠ECN时
∴CD=BD,
∵∠B+∠A=90°,∠ECN+∠ACD=90°,
∴∠A=∠ACD.
∴CD=AD.
∴AD=BD=![]() .
.
②当∠B=∠CNE时
∴NE∥AB.
∴∠ADC=∠CNE=90°.
∴∠ADC=∠ACB.
∵∠A=∠A,
∴△ACD∽△ABC,
∴![]() .
.
∴![]() .
.
(3)∵∠EDN=∠EDM,∠DNE=∠DME=90°,DE=DE,
∴△DNE≌△DME.
∵四边形MEND与△BDE的面积相等,
∴△DME与△BME的面积相等.
∴DM=BM.
∵EM⊥BD,
∴DE=BE.
∴∠B=∠BDE=∠CDE.
∵∠B=∠B,∠BME=∠ACB=90°,
∴△BME∽△BCA.
∴![]() .
.
∴![]() .
.
∵∠DCE=∠DCB,
∴△CDE∽△CBD.
∴![]() .
.
∴CD=![]() .
.
∴CE=![]() .
.
∴BD=![]() .
.
∴BE=![]() .
.
∴AD=AB-BD=5-![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园门票的收费标准如下:
门票类别
成人票
儿童票
团体票(限5张及以上)
价格(元/人)
100
40
60
有两个家庭分别去该公园游玩,每个家庭都有5名成员,且他们都选择了最省钱的方案购买门票,结果一家比另一家少花40元,则花费较少的一家花了_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 △ABC中,AB=AC=5,BC=6,AD⊥BC于D,点E,F分别在AD,AB是,则BE+EF的最小值是

A. 4 B. 4.8 C. 5 D. 5.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
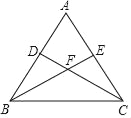
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P位于y轴右侧,距y轴3个单位长度,位于x轴上方,距离x轴4个单位长度,则点P坐标是( )
A.(3,4)B.(-3,4)C.(-4,3)D.(4,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点 A的坐标为(4,2),顶点B,C分别在
 轴,
轴, 轴的正半轴上.
轴的正半轴上.(1)求证:∠OCB=∠ABE;
(2)求OC长的取值范围;
(3)若D的坐标为(
 ,
, ),请说明
),请说明 随
随 的变化情况.
的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰三角形,AB=AC,∠A=36°.
(1)利用尺规作∠B的平分线BD,交AC于点D;(保留作图痕迹,不写作法)
(2)判断△BCD是否为等腰三角形,并说明理由.
相关试题

