搜索
【题目】如图，在 △ABC中，AB＝AC＝5，BC＝6，AD⊥BC于D，点E，F分别在AD，AB是，则BE＋EF的最小值是
A. 4 B. 4.8 C. 5 D. 5.4
参考答案：
【答案】B
【解析】作F关于AD的对称点M,连接BM交AD于E,连接EF,过B作BN⊥AC于N,已知AB＝AC＝5，BC＝6，AD⊥BC于D，根据等腰三角形的三线合一的性质可得 BD=CD=3，AD平分∠BAC,即可得点M在AC上,在Rt△ABD中，由勾股定理求得AD=4，所以
，由此求得BN=4.8，再由点F关于AD的对称点M可得EF=EM，所以 BE+EF=BE+EM=BM，根据垂线段最短得出:BM≥BN,即BE+EF≥4.8 ,即BE+EF 的最小值是4.8，故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】江夏某村种植的水稻2010年平均亩产500kg，2012年平均亩产605kg，求该村亩产量的年平均增长率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】钓鱼岛自古就是中国的领土，中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测．一日，中国一艘海监船从A点沿正北方向巡航，其航线距钓鱼岛（设M，N为该岛的东西两端点）最近距离为14.4km（即MC=14.4km）．在A点测得岛屿的西端点M在点A的北偏东42°方向；航行4km后到达B点，测得岛屿的东端点N在点B的北偏东56°方向，（其中N，M，C在同一条直线上），求钓鱼岛东西两端点MN之间的距离（结果精确到0.1km）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90，sin56°≈0.83，cos56°≈0.56，tan56°≈1.48）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公园门票的收费标准如下：
门票类别
成人票
儿童票
团体票（限5张及以上）
价格（元/人）
100
40
60
有两个家庭分别去该公园游玩，每个家庭都有5名成员，且他们都选择了最省钱的方案购买门票，结果一家比另一家少花40元，则花费较少的一家花了_____元．
-
科目： 来源： 题型：
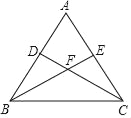
查看答案和解析>>【题目】如图，已知等腰三角形ABC中，AB=AC，点D、E分别在边AB、AC上，且AD=AE，连接BE、CD，交于点F．
（1）判断∠ABE与∠ACD的数量关系，并说明理由；
（2）求证：过点A、F的直线垂直平分线段BC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D在边AB上运动，DE平分∠CDB交边BC于点E，EM⊥BD于M，EN⊥DC于N．
(1)当AD＝CD时，求证DE//AC；
(2)当∠MBE与△CNE的某一个内角相等时，求AD的长；
(3)当四边形MEND与△BDE的面积相等时，求AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是( )
A.(3,4)B.(-3,4)C.(-4,3)D.(4，3)
相关试题
