【题目】21.(2013年四川攀枝花8分)某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元;
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案;
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大;最大利润是多少元.
参考答案:
【答案】(1)甲,乙两种钢笔每支各需5元和10元;(2)六种;(3)乙钢笔20支,甲钢笔160支时获利最大,最大利润为380元.
【解析】
(1)先设购进甲,乙两种钢笔每支各需a元和b元,根据购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元列出方程组,求出a,b的值即可.
(2)先设购进甲钢笔x支,乙钢笔y支,根据题意列出5x+10y=1000和不等式组6y≤x≤8y,把方程代入不等式组即可得出20≤y≤25,求出y的值即可.
(3)先设利润为W元,得出W=2x+3y=400﹣y,根据一次函数的性质求出最大值.
解:(1)设购进甲,乙两种钢笔每支各需a元和b元,根据题意得:
![]() ,解得:
,解得:![]() .,
.,
答:购进甲,乙两种钢笔每支各需5元和10元.
(2)设购进甲钢笔x支,乙钢笔y支,根据题意可得:
![]() ,解得:20≤y≤25.
,解得:20≤y≤25.
∵x,y为整数,∴y=20,21,22,23,24,25共六种方案.
∵5x=1000﹣10y>0,∴0<y<100.
∴该文具店共有6种进货方案.
(3)设利润为W元,则W=2x+3y,
∵5x+10y=1000,∴x=200﹣2y,代入上式得:W=400﹣y.
∵W随着y的增大而减小,
∴当y=20时,W有最大值,最大值为W=400﹣20=380(元).
即当乙钢笔20支,甲钢笔160支时获利最大,最大利润为380元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车从M地出发沿一条公路匀速前往N地,乙骑摩托车从N地出发沿同一条公路匀速前往M地,
已知乙比甲晚出发0.5小时且先到达目的地.设甲行驶的时间为t(h),甲乙两人之间的路程为y(km),
y与t的函数关系如图1所示,请解决以下问题:
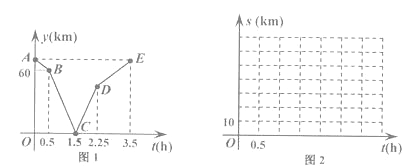
(1)写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式.
(2)①求点D的纵坐标.
②求M,N两地之间的距离.
(3)设乙离M地的路程为S乙 (km),请直接写出S甲 与时间t(h)的函数表达式,并在图2所给的直角坐标系中画出它的图象.
-
科目: 来源: 题型:
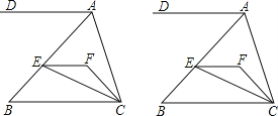
查看答案和解析>>【题目】 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.
(1)求∠FEC的度数;
(2)若∠BAC=3∠B,求证:AB⊥AC;
(3)当∠DAB=______度时,∠BAC=∠AEC.(请直接填出结果,不用证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(-
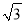 ,0),B(0,3),C(0,-1)三点.
,0),B(0,3),C(0,-1)三点.
(1)求线段BC的长度;
(2)若点D在直线AC上,且DB=DC,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个,黄球1个,从中任意摸出1球是黄球的概率是
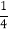 .
.(1)试求口袋中绿球的个数;
(2)小明第一次从口袋中任意摸出1球,不放回搅匀,第二次再摸出1球.请用列表或画树状图的方法求摸出“一绿一黄”的概率.
-
科目: 来源: 题型:
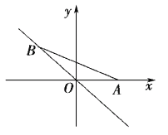
查看答案和解析>>【题目】如图,点A的坐标为(1,0),点B在直线y=-x上运动,当线段AB最短时,点B的坐标为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(-1,4),B(4,2),C(-1,0)三点.
(1)点A关于y轴的对称点A′ 的坐标为 ,点B关于x轴的对称点B′ 的坐标为 ,线段AC的垂直平分线与y轴的交点D的坐标为 ;
(2)求(1)中的△A′ B′ D的面积.
相关试题

