【题目】计算题。
(1)计算: ![]() .
.
(2)解不等式:4x+5≤2(x+1).
参考答案:
【答案】
(1)
解:原式=1+ ![]() -4-3
-4-3 ![]() =-3.
=-3.
(2)
解:4x+5≤2(x+1)
去括号,得4x+5≤2x+2
移项合并类项,得2x≤-3
解得x≤ ![]()
【解析】(1)所有非零数的0次幂的结果都为1,去绝对值符号时要注意非负性,化简二次根式 ![]() 可运用二次根式的乘法性质.(2)按解不等式的一般解法,去分母,再去括号,再移项并合并同类项,最后系数化为1.
可运用二次根式的乘法性质.(2)按解不等式的一般解法,去分母,再去括号,再移项并合并同类项,最后系数化为1.
【考点精析】利用二次根式的性质与化简对题目进行判断即可得到答案,需要熟知1、如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简.2、如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)已知A=3x2+4xy,B=x2+3xy--y2,求:-A+2B.
(2)先化简,再求值:2(5a2-7ab+9b2)-3(14a2-2ab+3b2),其中a=
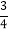 ,b=-
,b=- .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数
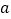 ,
, 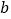 ,定义关于“
,定义关于“  ”的一种运算如下:
”的一种运算如下: 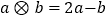 .例如:
.例如: 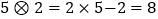 ,
, 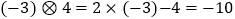 .
.
(1)若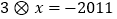 ,求
,求 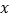 的值;
的值;
(2)若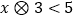 ,求
,求 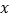 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=
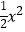 +bx+c的顶点,则抛物线y=
+bx+c的顶点,则抛物线y= 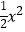 +bx+c与直线y=1交点的个数是( )
+bx+c与直线y=1交点的个数是( ) 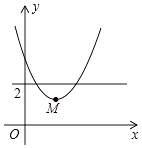
A.0个或1个
B.0个或2个
C.1个或2个
D.0个、1个或2个 -
科目: 来源: 题型:
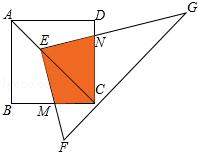
查看答案和解析>>【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A. a2
a2
B. a2
a2
C. a2
a2
D. a2
a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(﹣8,0),点P的坐标为
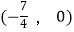 ,直线y=
,直线y=  x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.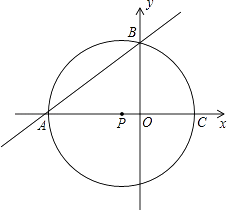
(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
相关试题

