【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线为AF,AF与CD交于点E,则△CEF是__________三角形.

参考答案:
【答案】等腰
【解析】
首先根据条件∠ACB=90°,CD是AB边上的高,可证出∠BCD+∠ACD=90°,∠B+∠BCD=90°,再根据同角的补角相等可得到∠B=∠DCA,再利用三角形的外角与内角的关系可得到∠CFE=∠FEC,最后利用等角对等边可证出结论.
∵∠ACB=90°,∴∠BCD+∠ACD=90°.
∵CD是AB边上的高,∴∠B+∠BCD=90°,∴∠B=∠DCA.
∵AF是∠BAC的平分线,∴∠1=∠2.
∵∠1+∠B=∠CFE,∠2+∠DCA=∠FEC,∴∠CFE=∠FEC,∴CF=CE,∴△CEF是等腰三角形.

故答案为:等腰.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点A、B分别是∠NOP、∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )

A. AD+BC=AB B. 与∠CBO互余的角有两个
C. ∠AOB=90° D. 点O是CD的中点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )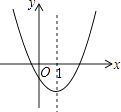
A.①②
B.①④
C.①③④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,有下列四个结论:①点P在∠BAC的平分线上;②AS=AR;③QP∥AB;④△BRP≌△CSP.其中,正确的有__________(填序号即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)用公式法解方程x2﹣3x﹣7=0.
(2)解方程:4x(2x﹣1)=3(2x﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】王师傅常用角尺平分一个角,如图所示,学生小明可用三角尺平分一个角,他们在∠AOB两边上分别取OM、ON,使OM=ON,前者使角尺两边相同刻度分别与M、N重合,角尺顶点为P;后者分别过M、N作OA、OB的垂线,交点为P,则均可得到△OMP≌△ONP,其依据分别是____________.

相关试题

