搜索
【题目】如图①是一块瓷砖的图案用这种瓷砖来铺设地面如果铺成一个2×2的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个3×3的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个4×4的正方形图案（如图④），其中完整的圆共有25个，若这样铺成一个15×15的正方形图案，则其中完整的圆共有（ ）个．
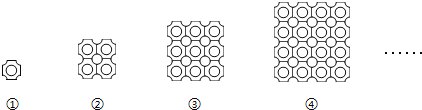
A.365B.366C.420D.421
参考答案：
【答案】D
【解析】
根据给出的四个图形的规律可以知道，组成大正方形的每个小正方形上有一个完整的圆，因此圆的数目是大正方形边长的平方，每四个小正方形组成一个完整的圆，从而可得这样的圆是大正方形边长减1的平方，从而可得若这样铺成一个15×15的正方形图案，则其中完整的圆共有2×152﹣2×15+1＝421个．
解：分析可得：组成大正方形的每个小正方形上有一个完整的圆，因此圆的数目是大正方形边长的平方，即为n2；
又每四个小正方形组成一个完整的圆，这样的圆的个数是大正方形边长减1的平方，即为（n﹣1）2，
∴若这样铺成一个n×n的正方形图案，所得到的完整圆的个数共有：n2+（n﹣1）2＝2n2﹣2n+1
当n＝15时，2×152﹣2×15+1＝421
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。
现有19张硬纸板，裁剪时
张用A方法，其余用B方法。（1）用
的代数式分别表示裁剪出的侧面和底面的个数；（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于平面直角坐标系中的任意两点P1（x1，y1），P2（x2，y2），我们把
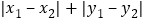叫做P1、P2两点间的直角距离，记作d（P1，P2）．（1）已知O为坐标原点，动点P（x，y）满足d（O，P）=1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；
（2）设P0（x0，y0）是一定点，Q（x，y）是直线y=ax+b上的动点，我们把d（P0，Q）的最小值叫做P0到直线y=ax+b的直角距离．试求点M（2，1）到直线y=x+2的直角距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（14分）如图，二次函数y=-
x2+bx+c的图像经过点A（4,0）B（-4，-4），且与y轴交于点C．
（1）求此二次函数的解析式；
（2）证明：∠BAO=∠CAO（其中O是原点）；
（3）若P是线段AB上的一个动点（不与A、B重合），过P作y轴的平行线，分别交此二次函数图像及x轴于Q、H两点，试问：是否存在这样的点 P，使PH=2QH？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣．已知购买甲型机器人1台，乙型机器人2台，共需14万元；购买甲型机器人2台，乙型机器人3台，共需24万元．
（1）求甲、乙两种型号的机器人每台的价格各是多少万元；
（2）已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件，该公司计划购买这两种型号的机器人共8台，总费用不超过41万元，并且使这8台机器人每小时分拣快递件数总和不少于8300件，则该公司有哪几种购买方案？哪个方案费用最低，最低费用是多少万元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校在3月份举行读书节活动，鼓励学生进行有益的课外阅读，张老师为了了解该校学生课外阅读的情况，设计了“你最喜欢的课外读物类型”的调查问卷，包括“名著”“科幻”“历史”“童话”四类，在学校随机抽取了部分学生进行调查，被抽取的学生只能在四种类型中选择其中一类，最后将调查结果绘制成如下两幅尚不完整的统计图.
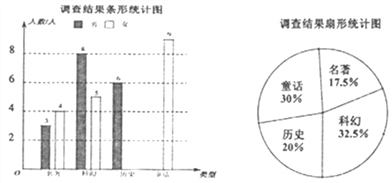
请你根据以上信息解答下列问题：
（1）本次调查中，张老师一共调查了 名学生；
(2)求本次调查中选择“历史”类的女生人数和“童话”类的男生人数，并将条形统计图补充完整；
(3)扇形图中“童话”类对应的圆心角度数为 .
(4)如果该校共有学生360名，请估算该校最喜欢“名著”类和“历史”类的学生总人数.
-
科目： 来源： 题型：
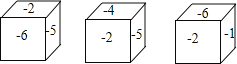
查看答案和解析>>【题目】一个正方体的六个面上分别标有﹣1，﹣2，﹣3，﹣4，﹣5，﹣6中的一个数，各个面上所标数字都不相同，如图是这个正方体的三种放置方法，三个正方体下底面所标数字分别是a，b，c，则a+b+c+abc＝_____．
相关试题
