【题目】一艘快艇从A码头到B码头顺流行驶,同时一艘游船从B码头出发逆流行驶.已知,A、B两码头相距140千米,快艇在静水中的平均速度为67千米/小时,游船在静水中的平均速度为27千米/小时,水流速度为3千米/小时。
(1)请计算两船出发航行30分钟时相距多少千米?
(2)如果快艇到达B码头后立即返回,试求快艇在返回的过程中需航行多少时间两船恰好相距12千米?
参考答案:
【答案】(1)在航行30分钟时两船相距93千米;(2)快艇在返回的过程中需航行![]() 或
或![]() 小时两船恰好相距12千米.
小时两船恰好相距12千米.
【解析】试题分析:(1)分别求出快船顺流速度和游艇逆流速度,则两车30分钟后相距距离为开始总距离-快艇路程-游艇路程即可;(2)分两种情况讨论:①快艇返回时,两船未相遇,相距12千米;②快艇返回时,两船相遇后,相距12千米.
解:(1)140-(67+3)×![]() -(27-3)×
-(27-3)×![]() =93(千米).
=93(千米).
即航行30分钟时两船相距93千米;
(2)设快艇在返回的过程中需航行x小时两船恰好相距12千米.
由快艇从A到达B码头时,用时140÷(67+3)=2(时),
此时游艇行驶2×(27-3)=48(千米).且返回时快艇速度为67-3=64(千米/时),
①快艇返回时,两船未相遇,相距12千米,
则48+24x-64x=12,解得x=![]() .
.
②快艇返回时,两船相遇后,相距12千米.
则64x-(48+24x)=12,解得x=![]() .
.
此时![]() ×64=96(千米),即快艇未到达A码头,符合题意.
×64=96(千米),即快艇未到达A码头,符合题意.
答:快艇在返回的过程中需航行![]() 或
或![]() 小时两船恰好相距12千米.
小时两船恰好相距12千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】70°30′的余角为°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方形截去(至少)一个角,则其边数_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=4是一元二次方程x2-x+m=0的一个根,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )

A.SAS
B.ASA
C.AAS
D.SSS -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( )
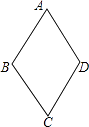
A.52cm
B.40cm
C.39cm
D.26cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如果2△3=2+3+4, 5△4=5+6+7+8,且1△x=15, 求x。
相关试题

