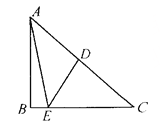
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )

A. 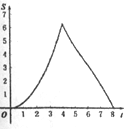 B.
B. 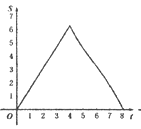
C. 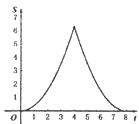 D.
D. 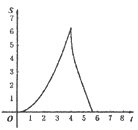
参考答案:
【答案】C
【解析】∵Rt△ABC中,∠A=90°,AB=AC=4,点E以每秒1个单位的速度从点C出发,
∴当0≤t≤4时,扇形面积S=![]() ,
,
∴前半段函数图象为开口向上的抛物线的一部分,故B选项错误;
当4<t≤8时,随着t的增大,扇形的半径增大,而扇形的圆心角减小,
∴后半段函数图象不是抛物线,故C选项错误;
∵当t=8时,点E、D重合,
∴扇形的面积为0,故D选项错误;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一小长假,李军与张明相约去宁波旅游,李军从温岭北上沿海高速,同时张明从玉环芦浦上沿海高速,温岭北与玉环芦浦相距44千米,两人约好在三门服务区集合,李军由于离三门近,行驶了1.2小时先到达三门服务站等候张明,张明走了1.4小时到达三门服务站。在整个过程中,两人均保持各自的速度匀速行驶,两人相距的路程y千米与张明行驶的时间x小时的关系如图所示,下列说法错误的是( )
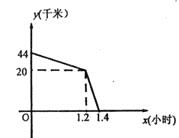
A.李军的速度是80千米/小时
B.张明的速度是100千米/小时
C.玉环芦浦至三门服务站的路程是140千米
D.温岭北至三门服务站的路程是44千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列条件,能画出唯一△ABC的是( )
A.AB=4,BC=5,AC=1B.AB=5,BC=4,∠A=40°
C.∠A=60°,∠B=50°,AB=5D.∠C=90°,AB=8
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
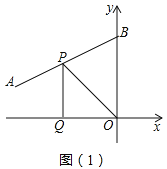
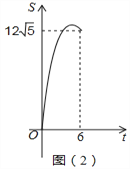
如图(1),线段AB的两个端点的坐标分别为(-12,4)(0,10),点P从点B出发,沿BA方向匀速向点A运动;同时,点Q从坐标原点O出发,沿x轴的反方向以相同的速度运动,当点P到达点A时,P,Q两点同时停止运动,设运动的时间为t秒,ΔOPQ的面积S(平方单位)与时间t(秒)之间的函数图象如图(2)所示。
(1)求点P的运动速度;
(2)求面积S与t的函数关系式及当S最最大值时点P的坐标;
(3)点P是S取最大值时的点,设点M为x轴上的点,点N为坐标平面内的点,以点O,P,M,N为顶点的四边形地矩形,请直接写出点N的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=2x+l与双曲线y=
 的一个交点为A(m,-3).
的一个交点为A(m,-3).(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=
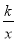 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C=_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?

相关试题

