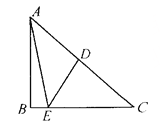
【题目】如图,在Rt△ABC中,B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C=_________.
参考答案:
【答案】40°
【解析】
根据线段垂直平分线的性质得到EA=EC,则∠EAC=∠C,设∠BAE=x,则∠BAC=5x,则∠C=∠EAC=∠BAC-∠BAE=4x,根据三角形内角和定理得到4x+5x+90°=180°,解得x=10°,利用∠C=4x即可得到∠C的度数.
∵DE是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
设∠BAE=x,则∠BAC=5x,
∴∠EAC=∠BAC-∠BAE=4x,
∴∠C=4x,
∴4x+5x+90°=180°,解得x=10°,
∴∠C=4x=40°.
故答案为40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
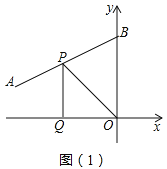
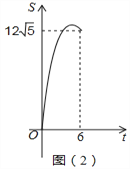
如图(1),线段AB的两个端点的坐标分别为(-12,4)(0,10),点P从点B出发,沿BA方向匀速向点A运动;同时,点Q从坐标原点O出发,沿x轴的反方向以相同的速度运动,当点P到达点A时,P,Q两点同时停止运动,设运动的时间为t秒,ΔOPQ的面积S(平方单位)与时间t(秒)之间的函数图象如图(2)所示。
(1)求点P的运动速度;
(2)求面积S与t的函数关系式及当S最最大值时点P的坐标;
(3)点P是S取最大值时的点,设点M为x轴上的点,点N为坐标平面内的点,以点O,P,M,N为顶点的四边形地矩形,请直接写出点N的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )

A.
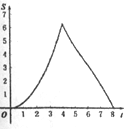 B.
B. 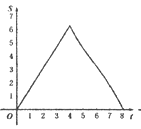
C.
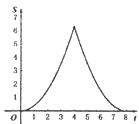 D.
D. 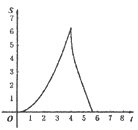
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=2x+l与双曲线y=
 的一个交点为A(m,-3).
的一个交点为A(m,-3).(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+l和双曲线y=
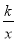 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
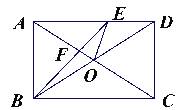
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:
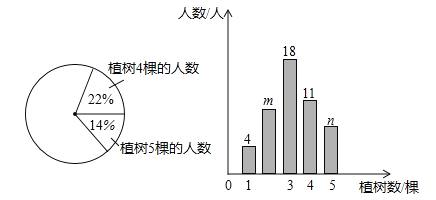
(1)八年级三班共有多少名同学?
(2)条形统计图中,m= ,n= .
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
相关试题

