搜索
【题目】在2018年韶关市开展的“善美韶关情暖三江”的志愿者系列括动中，某志愿者组织筹集了部分资金，计划购买甲、乙两种书包若干个送给贫困山区的学生，已知每个甲种书包的价格比每个乙种书包的价格贵10元，用350元购买甲种书包的个数恰好与用300元购买乙种书包的个数相同，求甲、乙两种书包每个的价格各是多少元？
参考答案：
【答案】每件乙种商品的价格为60元，每件甲种商品的价格为70元
【解析】
设每件甲种商品的价格为x元，则每件乙种商品的价格为（x-10）元，根据数量=总价÷单价结合用350元购买甲种书包的个数恰好与用300元购买乙种书包的个数相同，即可得出关于x的分式方程，解之并检验后即可得出结论.
解：
设每件甲种商品的价格为x元，则每件乙种商品的价格为（x﹣10）元，
根据题意得：
，
解得：x=70，
经检验，x=70是原方程的解，
∴x﹣10=60．
答：每件乙种商品的价格为60元，每件甲种商品的价格为70元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知某种产品的进价为每件40元，现在的售价为每件60元，每星期可卖出300件．市场调查发现，该产品每降价1元，每星期可多卖出20件，由于供货方的原因销量不得超过380件，设这种产品每件降价x元（x为整数），每星期的销售利润为w元．
（1）求w与x之间的函数关系式，并写出自变量x的取值范围；
（2）该产品销售价定为每件多少元时，每星期的销售利润最大？最大利润是多少元？
（3）该产品销售价在什么范围时，每星期的销售利润不低于6000元，请直接写出结果．
-
科目： 来源： 题型：
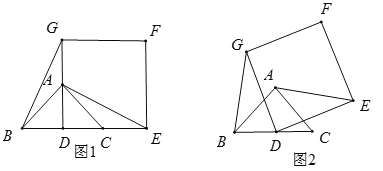
查看答案和解析>>【题目】(1)观察猜想
如图(1)，在△ABC中，∠BAC=90°，AB=AC,点D是BC的中点．以点D为顶点作正方形DEFG，使点A，C分别在DG和DE上，连接AE，BG，则线段BG和AE的数量关系是_____；
(2)拓展探究
将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，小于或等于360°），如图2，则(1)中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由.
(3)解决问题
若BC=DE=2，在(2)的旋转过程中，当AE为最大值时，直接写出AF的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
经过点E（1，0）和F（5，0），并交y轴于D（0，-5）；抛物线
：
（a≠0），（1）试求抛物线
的函数解析式；（2）求证： 抛物线
与x轴一定有两个不同的交点；（3）若a=1
①抛物线
、顶点分别为 （ ， ）、（ ， ） ；当x的取值范围是_________ 时，抛物线、 上的点的纵坐标同时随横坐标增大而增大；②已知直线MN分别与x轴、
、分别交于点P（m，0）、M、N，且MN∥y轴，当1≤m≤5时，求线段MN的最大值。 -
科目： 来源： 题型：
查看答案和解析>>【题目】“端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A、B、C、D表示）这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．
请根据以上信息回答：
（1）本次参加抽样调查的居民有多少人？
（2）将两幅不完整的图补充完整；
（3）若居民区有8000人，请估计爱吃D粽的人数；
（4）若有外型完全相同的A、B、C、D粽各一个，煮熟后，小王吃了两个．用列表或画树状图的方法，求他第二个吃到的恰好是C粽的概率．
-
科目： 来源： 题型：
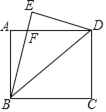
查看答案和解析>>【题目】如图，将矩形ABCD沿对角线BD折叠，使点C落在点E处，BE与AD交于点F．
（1）求证：△ABF≌△EDF；
（2）若AB=6，BC=8，求AF的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】因为一次函数
与
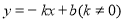的图象关于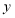
轴对称，所以我们定义:函数与互为
“镜子”函数.(1)请直接写出函数
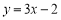的“镜子”函数：________.(2)如图，一对“镜子”函数
与的图象交于点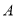
，分别与
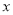轴交于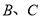
两点，且AO=BO，△ABC的面积为
，求这对“镜子”函数的解析式.
相关试题
