【题目】因为一次函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数![]() 与互为
与互为![]() “镜子”函数.
“镜子”函数.
(1)请直接写出函数![]() 的“镜子”函数:________.
的“镜子”函数:________.
(2)如图,一对“镜子”函数![]() 与
与![]() 的图象交于点
的图象交于点![]() ,分别与
,分别与![]() 轴交于
轴交于![]() 两点,且AO=BO,△ABC的面积为
两点,且AO=BO,△ABC的面积为![]() ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.

参考答案:
【答案】(1)y=-3x-2;(2)![]() ;
;![]() .
.
【解析】
(1)根据“镜子”函数的定义解答即可;
(2)根据“镜子”函数的定义可得![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,即可得出AO=BO=CO,设OA=OB =OC=x,根据△ABC的面积为
轴对称,即可得出AO=BO=CO,设OA=OB =OC=x,根据△ABC的面积为![]() 列方程求出x的值,即可得点A、B、C的坐标,利用待定系数法求出k、b的值即可得答案.
列方程求出x的值,即可得点A、B、C的坐标,利用待定系数法求出k、b的值即可得答案.
(1)∵函数![]() 与互为
与互为![]() “镜子”函数.
“镜子”函数.
∴函数![]() 的“镜子”函数是
的“镜子”函数是![]() ,
,
故答案为:![]()
(2)∵函数![]() 与
与![]() 是一对“镜子”函数,
是一对“镜子”函数,
∴一次函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,
轴对称,
∴BO=CO,
∴AO=BO=CO,
设![]() ,根据题意可得
,根据题意可得![]()
解得![]()
∴![]() ,
,![]()
将B、A的坐标分别代入![]() 中得
中得![]() ,
,
解得:![]()
∴其函数解析式为![]() ,
,
∴其“镜子”函数解析式为![]() .
.
∴这对“镜子”函数的解析式为![]() 和
和![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2018年韶关市开展的“善美韶关情暖三江”的志愿者系列括动中,某志愿者组织筹集了部分资金,计划购买甲、乙两种书包若干个送给贫困山区的学生,已知每个甲种书包的价格比每个乙种书包的价格贵10元,用350元购买甲种书包的个数恰好与用300元购买乙种书包的个数相同,求甲、乙两种书包每个的价格各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
-
科目: 来源: 题型:
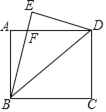
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)求证:△ABF≌△EDF;
(2)若AB=6,BC=8,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为奖励学习之星,准备在某商店购买A、B两种文具作为奖品,已知一件A种文具的价格比一件B种文具的价格便宜5元,且用600元买A种文具的件数是用400元买B种文具的件数的2倍.
(1)求一件A种文具的价格;
(2)根据需要,该校准备在该商店购买A、B两种文具共150件.
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式;
②若购买A种文具的件数不多于B种文具件数的2倍,且计划经费不超过2750元,求有几种购买方案,并找出经费最少的方案,及最少需要多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段a、b、c.分别为△ABC中∠A、∠B、∠C的对边,下列不能构成直角三角形的是( )
A.a=5,b=12,c=13B.a=b=5,c=5
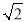
C.∠A:∠B:∠C=3:4:5D.∠A+∠B+
 ∠C=135°
∠C=135° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
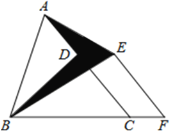
A.3B.4C.6D.8
相关试题

