【题目】填空,如图所示.

(1)∵![]() (已知),∴_________
(已知),∴_________![]() _________ (______).
_________ (______).
(2)∵![]() (已知),∴_________
(已知),∴_________![]() _________(______).
_________(______).
(3)∵![]() _________
_________![]() (已知),∴
(已知),∴![]() (______).
(______).
参考答案:
【答案】CD AB 内错角相等,两直线平行 BD AC 同位角相等,两直线平行 ![]() 同旁内角互补,两直线平行
同旁内角互补,两直线平行
【解析】
(1)根据平行线的判定定理:内错角相等,两直线平行分析即可;
(2)根据平行线的判定定理:同位角相等,两直线平行分析即可;
(3)根据平行线的判定定理:同旁内角互补,两直线平行分析即可.
解:(1)∵![]() (已知),
(已知),
∴CD![]() AB(内错角相等,两直线平行)
AB(内错角相等,两直线平行)
故答案为:CD;AB;内错角相等,两直线平行;
(2)∵![]() (已知),
(已知),
∴BD![]() AC(同位角相等,两直线平行)
AC(同位角相等,两直线平行)
故答案为:BD;AC;同位角相等,两直线平行;
(3)∵![]()
![]()
![]() (已知),
(已知),
∴![]() (同旁内角互补,两直线平行).
(同旁内角互补,两直线平行).
故答案为:![]() ;同旁内角互补,两直线平行.
;同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若
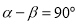 ,且
,且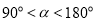 ,则我们称
,则我们称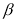 是
是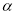 的差余角.例如:若
的差余角.例如:若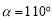 ,则
,则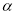 的差余角
的差余角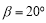 .
.(1)如图1,点
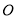 在直线
在直线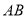 上,射线
上,射线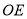 是
是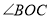 的角平分线,若
的角平分线,若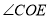 是
是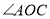 的差余角,求
的差余角,求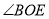 的度数.
的度数.(2)如图2,点
 在直线
在直线 上,若
上,若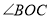 是
是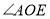 的差余角,那么
的差余角,那么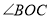 与
与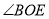 有什么数量关系.
有什么数量关系.(3)如图3,点
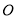 在直线
在直线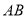 上,若
上,若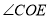 是
是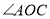 的差余角,且
的差余角,且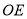 与
与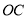 在直线
在直线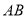 的同侧,请你探究
的同侧,请你探究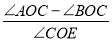 是否为定值?若是,请求出定值;若不是,请说明理由.
是否为定值?若是,请求出定值;若不是,请说明理由.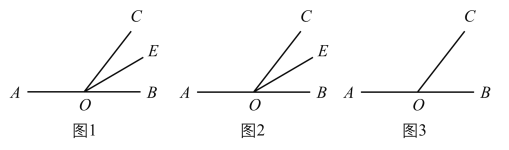
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形,它是把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,将这种做法继续下去(如图2,图3…).观察规律解答以下各题:
 ……
……(1)填写下表:
图形序号
挖去三角形的个数
图1
1
图2
1+3
图3
1+3+9
图4
(2)根据这个规律,求图n中挖去三角形的个数fn(用含n的代数式表示);
(3)若图n+1中挖去三角形的个数为fn+1,求fn+1-fn
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.
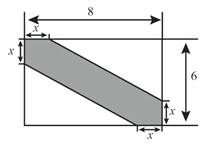
-
科目: 来源: 题型:
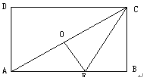
查看答案和解析>>【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
A.
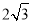 B.
B. 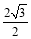 C.
C. 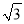 D. 6
D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
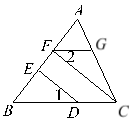
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
相关试题

