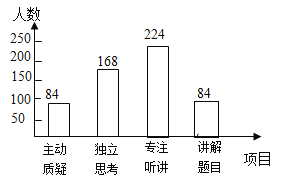
【题目】初二年级教师对试卷讲评课中学生参与情况进行调查,调查项目分为主动质疑、独立思考、专注听讲、讲解题目四项.调查组随机抽取了若干名初中学生的参与情况,绘制了如图所示的扇形统计图和条形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为______度;
(2)请将频数分布直方图补充完整;
(3)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
参考答案:
【答案】(1) 54;(2)补全频数分布直方图见解析;(3)在试卷评讲课中,“独立思考”的初二学生约有1800人.
【解析】
(1)根据专注听讲的人数是224人,所占的比例是40%,即可求得抽查的总人数,继而用360°乘以“主动质疑”的人数所占比例可得答案;
(2)利用总人数减去其他各组的人数,即可求得讲解题目的人数,从而作出频数分布直方图;
(3)利用6000乘以对应的比例即可.
(1)调查的总人数为224÷40%=560(人),∴项目“主动质疑”所在的扇形的圆心角的度数为360°![]() 54°.
54°.
故答案为:54;
(2)选择“讲解题目”的人数为560﹣84﹣168﹣224=84(人),补全频数分布直方图如下:
(3)![]() 6000=1800(人).
6000=1800(人).
答:在试卷评讲课中,“独立思考”的初二学生约有1800人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读可以增进人们的知识,也能陶冶人们的情操.我们要多阅读有营养的书.某校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
阅读时间分组统计表
组别
阅读时间x(h)
人数
A
0≤x<10
a
B
10≤x<20
100
C
20≤x<30
b
D
30≤x<40
140
E
x≥40
c
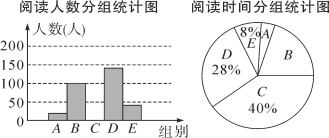
请结合以上信息解答下列问题:
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=
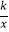 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:两位同学在用标有数字1,2,...,9的9张卡片做游戏.
甲同学:“你先从这9张卡片中随意抽取两张(按抽取的先后顺序分别称为“卡片
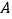 ”和“卡片
”和“卡片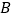 ”),别告诉我卡片上是什么数字,然后你把卡片
”),别告诉我卡片上是什么数字,然后你把卡片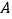 上的数字乘以5,加上7,再乘以2,再加上卡片
上的数字乘以5,加上7,再乘以2,再加上卡片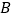 上的数字,把最后得到的数
上的数字,把最后得到的数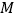 的值告诉我,我就能猜出你抽出的是哪两张卡片啦!”
的值告诉我,我就能猜出你抽出的是哪两张卡片啦!”乙同学:“这么神奇?我不信.”
……
试验一下:
(1)如果乙同学抽出的卡片
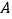 上的数字为2,卡片
上的数字为2,卡片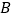 上的数字为5,他最后得到的数
上的数字为5,他最后得到的数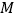 等于多少;
等于多少;(2)若乙同学最后得到的数
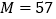 ,则卡片
,则卡片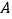 上的数字为多少,卡片
上的数字为多少,卡片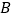 上的数字为多少.
上的数字为多少.解密:
请你说明:对任意告知的数
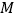 ,甲同学是如何猜到卡片的.
,甲同学是如何猜到卡片的.解:(1)
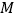 等于多少.
等于多少.(2)若
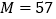 ,则卡片
,则卡片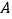 上的数字为多少,卡片
上的数字为多少,卡片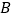 上的数字为多少.
上的数字为多少.解密:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设
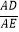 =n.
=n.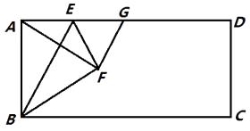
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示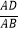 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(组)解决问题
某校初一年级组织了数学嘉年华活动,同学们踊跃参加,活动共评出三个奖项,年级购买了一些奖品进行表彰.为此,组织活动的老师设计了如下表格进行统计.
一等奖
二等奖
三等奖
合计
获奖人数(单位:人)
40
奖品单价(单位:元)
4
3
2

奖品金额(单位:元)
100
已知获得二等奖的人数比一等奖的人数多5人.问:获利三种奖项的同学各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )
A. (4,﹣3) B. (﹣4,3) C. (﹣3,4) D. (﹣3,﹣4)
相关试题

