搜索
【题目】列方程（组）解决问题
某校初一年级组织了数学嘉年华活动，同学们踊跃参加，活动共评出三个奖项，年级购买了一些奖品进行表彰.为此，组织活动的老师设计了如下表格进行统计.
一等奖 | 二等奖 | 三等奖 | 合计 | |
获奖人数（单位：人） | 40 | |||
奖品单价（单位：元） | 4 | 3 | 2 |
|
奖品金额（单位：元） | 100 |
已知获得二等奖的人数比一等奖的人数多5人.问：获利三种奖项的同学各多少人？
参考答案：
【答案】获得一等奖的同学有5人，获得二等奖的同学有10人，获得三等奖的同学有25人.
【解析】
设一等奖的人数有x人，根据二等奖的人数比一等奖的人数多5人，得出二等奖的人数，再根据总人数表示出三等奖的人数，最后根据奖品单价列出方程，然后求解即可得出答案．
设获得一等奖的同学有
人.
可填表如下：
一等奖 | 二等奖 | 三等奖 | 合计 | |
获奖人数（单位：人） |
|
|
| 40 |
奖品单价（单位：元） | 4 | 3 | 2 |
|
奖品金额（单位：元） |
|
|
| 100 |
根据题意列方程，得
.
去括号，得
.
移项，得
.
合并，得
.
系数化为1，得
.
所以
，
.
答：获得一等奖的同学有5人，获得二等奖的同学有10人，获得三等奖的同学有25人.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：两位同学在用标有数字1，2，...，9的9张卡片做游戏.
甲同学：“你先从这9张卡片中随意抽取两张（按抽取的先后顺序分别称为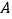“卡片
”和“卡片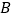
”），别告诉我卡片上是什么数字，然后你把卡片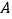上的数字乘以5，加上7，再乘以2，再加上卡片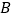上的数字，把最后得到的数
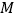的值告诉我，我就能猜出你抽出的是哪两张卡片啦！”乙同学：“这么神奇？我不信.”
……
试验一下：
（1）如果乙同学抽出的卡片
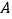上的数字为2，卡片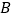上的数字为5，他最后得到的数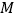等于多少；（2）若乙同学最后得到的数
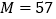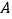，则卡片上的数字为多少，卡片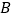上的数字为多少.解密：
请你说明：对任意告知的数
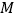，甲同学是如何猜到卡片的.解：（1）
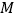等于多少.（2）若
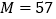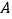，则卡片上的数字为多少，卡片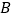上的数字为多少.解密：
-
科目： 来源： 题型：
查看答案和解析>>【题目】初二年级教师对试卷讲评课中学生参与情况进行调查，调查项目分为主动质疑、独立思考、专注听讲、讲解题目四项．调查组随机抽取了若干名初中学生的参与情况，绘制了如图所示的扇形统计图和条形统计图（均不完整），请根据图中所给信息解答下列问题：
(1)在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为______度；
(2)请将频数分布直方图补充完整；
(3)如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初二学生约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连结AF，BF，EF，过点F作GF⊥AF交AD于点G，设
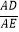=n.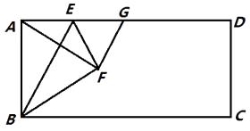
（1）求证：AE=GE；
（2）当点F落在AC上时，用含n的代数式表示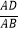
的值；
（3）若AD=4AB，且以点F，C，G为顶点的三角形是直角三角形，求n的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，以原点为旋转中心，把点A（3，4）逆时针旋转90°，得到点B，则点B的坐标为（ ）
A. （4，﹣3） B. （﹣4，3） C. （﹣3，4） D. （﹣3，﹣4）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一组密码的一部分，请你运用所学知识找到破译的“钥匙”．目前，已破译出“正做数学”的真实意思是“祝你成功”．若“正”所处的位置为（x，y），你找到的密码钥匙是：横坐标_____，纵坐标_____，破译的“今天考试”真实意思是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(本题6分)如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A(2，2)，B(4,1），C(4,4)．
（1）作出
ABC关于原点O成中心对称的 A1B1C1.
（2）作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部（不包括顶点和边界），求a的取值范围.
相关试题
