【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
参考答案:
【答案】(1![]() 种商品每件的进价是50元,
种商品每件的进价是50元,![]() 种商品每件的进价是30元;(2)商店共有5种进货方案;(3)①当
种商品每件的进价是30元;(2)商店共有5种进货方案;(3)①当![]() 时,获利最大,即买18件
时,获利最大,即买18件![]() 商品,22件
商品,22件![]() 商品,②当
商品,②当![]() 时,
时,![]() ,(2)问中所有进货方案获利相同,③当
,(2)问中所有进货方案获利相同,③当![]() 时,获利最大,即买14件
时,获利最大,即买14件![]() 商品,26件
商品,26件![]() 商品.
商品.
【解析】
(1)设A商品每件进价为x元,B商品每件的进价为(x-20)元,根据![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同,列方程求解;
种商品的数量相同,列方程求解;
(2)设购买![]() 种商品
种商品![]() 件,则购买
件,则购买![]() 商品(
商品(![]() )件,根据商店计划用不超过1560元的资金购进
)件,根据商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,列出不等式组即可
种商品数量的一半,列出不等式组即可
(3)先设销售![]() 两种商品共获利
两种商品共获利![]() 元,然后分析求解新的进货方案
元,然后分析求解新的进货方案
(1)设![]() 种商品每件的进价是
种商品每件的进价是![]() 元,则
元,则![]() 种商品每件的进价是
种商品每件的进价是![]() 元,
元,
由题意得:![]() ,
,
解得:![]() ,
,
经检验,![]() 是原方程的解,且符合题意,
是原方程的解,且符合题意,
![]() ,
,
答:![]() 种商品每件的进价是50元,
种商品每件的进价是50元,![]() 种商品每件的进价是30元;
种商品每件的进价是30元;
(2)设购买![]() 种商品
种商品![]() 件,则购买
件,则购买![]() 商品(
商品(![]() )件,
)件,
由题意得: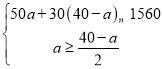 ,
,
解得:![]() ,
,
∵![]() 为正整数,
为正整数,
∴![]() 14、15、16、17、18,
14、15、16、17、18,
∴商店共有5种进货方案;
(3)设销售![]() 两种商品共获利
两种商品共获利![]() 元,
元,
由题意得:![]()
![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而增大,
的增大而增大,
∴当![]() 时,获利最大,即买18件
时,获利最大,即买18件![]() 商品,22件
商品,22件![]() 商品,
商品,
②当![]() 时,
时,![]() ,
,
![]() 与
与![]() 的值无关,即(2)问中所有进货方案获利相同,
的值无关,即(2)问中所有进货方案获利相同,
③当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,获利最大,即买14件
时,获利最大,即买14件![]() 商品,26件
商品,26件![]() 商品.
商品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=4﹣x与双曲线y
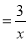 交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
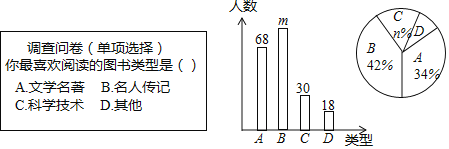
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4
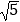 ,求tan∠BAD的值.
,求tan∠BAD的值. 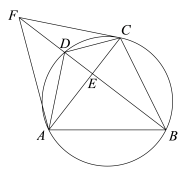
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC=20,tanB=
 ,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
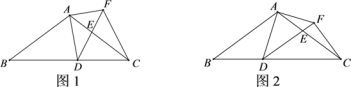
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线
 过点
过点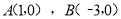 .
.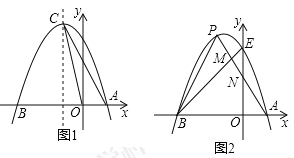
(1)求抛物线的解析式及其顶点C的坐标;
(2)设点D是x轴上一点,当
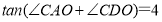 时,求点D的坐标;
时,求点D的坐标;(3)如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,
 和
和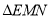 的面积分别为
的面积分别为 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点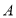 、
、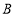 的坐标分别为
的坐标分别为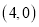 、
、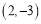 ,
,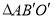 是
是 关于点
关于点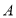 的位似图形,点
的位似图形,点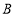 的对应点为点
的对应点为点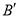 ,且
,且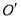 的坐标为
的坐标为 ,则点
,则点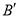 的坐标为( )
的坐标为( )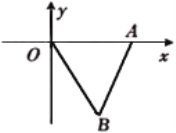
A.
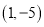 B.
B.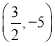 C.
C.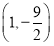 D.
D.
相关试题

