【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合)将△BCP沿CP所在的直线翻折,得到![]() ,连接
,连接![]() ,下面有四个判断:
,下面有四个判断:
①当AP=BP时,![]() ∥CP;
∥CP;
②当AP=BP时,![]()
③当CP⊥AB时,![]() ;
;
④![]() 长度的最小值是1.
长度的最小值是1.
所有正确结论的序号是( )
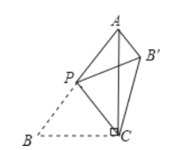
A.①③④B.①②C.①②④D.②③④
参考答案:
【答案】C
【解析】
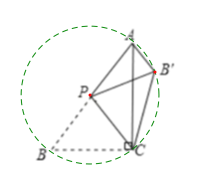
①由直角三角形斜边上的中线等于斜边的一半以及折叠的性质,易得∠AB′P=∠CPB′,即可得AB′∥CP;②由PA=PB′=PC=PB,可得点A,B′,C,B在以P为圆心,PA长为半径的圆上,然后由圆周角定理,求得答案;③当CP⊥AB时,易证得△ACP∽△ABC,然后由相似三角形的对应边成比例,求得AP的长;④易得当B′在线段AC上时,AB′的长度有最小值,继而求得答案.
∵在△ABC中,∠ACB=90°,AP=BP,
∴AP=BP=CP,
由折叠的性质可得:CP=B′P,∠CPB′=∠BPC=![]() (180°∠APB′),
(180°∠APB′),
∴AP=B′P,
∴∠AB′P=′B′AP=![]() (180°∠APB′),
(180°∠APB′),
∴∠AB′P=∠CPB′,
∴AB′∥CP,故①正确;
②∵在△ABC中,∠ACB=90°,AP=BP,将△BCP沿CP所在的直线翻折,得到![]() ,
,
∴PA=PB′=PC=PB,
∴点A,B′,C,B在以P为圆心,PA长为半径的圆上,
∵∠B′PC与∠B′AC是![]() 所对的圆心角和圆周角,
所对的圆心角和圆周角,
∴∠B′PC=2∠B′AC,故②正确;
③当CP⊥AB时,∠APC=∠ACB,
∵∠PAC=∠CAB,
∴△ACP∽△ABC,
∴![]() ,
,
∵在Rt△ABC中,AC=![]() =4,
=4,
∴AP=![]() =
=![]() ,故③错误;
,故③错误;
④由轴对称的性质可知:BC=CB′=3,
∴CB′长度固定不变,
∵在 AB′C中,AB′>ACB′C,
∴当B′在线段AC上时, AB′有最小值,此时,AB′=ACB′C=43=1,故④正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:在平面直角坐标系中,抛物线
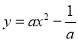 与
与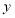 轴交于点
轴交于点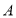 ,点
,点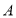 关于
关于 轴的对称点为点
轴的对称点为点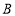 ,
,(1)求抛物线的对称轴;
(2)求点
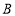 坐标(用含
坐标(用含 的式子表示);
的式子表示);(3)已知点
 ,
, ,若抛物线与线段
,若抛物线与线段 恰有一个公共点,结合函数图像,求
恰有一个公共点,结合函数图像,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=AC, ∠BAC <60°,将线段 AB 绕点 A逆时针旋转 60°得到点 D, 点 E 与点 D 关于直线 BC 对称,连接 CD,CE,DE.
(1)依题意补全图形;
(2)判断△CDE 的形状,并证明;
(3)请问在直线CE上是否存在点 P,使得 PA - PB =CD 成立?若存在,请用文字描述出点 P 的准确位置,并画图证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全国人民每天都很关心新型冠状病毒感染肺炎的全国疫情和湖北疫情,下面是2020年2月7日小明在网上看到的2020年2月6日有关全国和武汉的疫情统计图表:
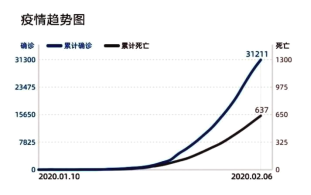
图1全国疫情趋势图
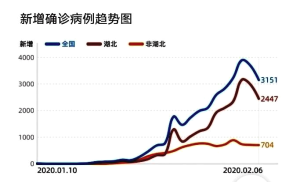
图2新增确诊病例趋势图
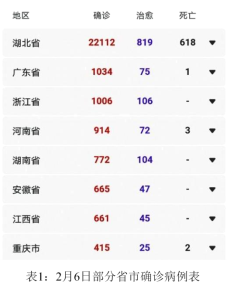
根据统计图表提供的信息,下列推断不合理的是( )
A.从图1可得出在2月6日的全国确诊病例达到3万多,是“非典”确诊病例(共5327例)的若干倍,说明新型冠状病毒比“非典”病毒传染性强.
B.从图2可得出在2月6日新增病例出现下降,说明此时全国的累计确诊病例开始下降,肺炎疫情得到控制,政府和人民的防疫工作有了显著成效
C.从图2在2月6日新增病例出现下降,可以估计2月6日后全国新型冠状病毒肺炎累计确诊病例的单日增长率会低于10%.
D.从表1可看出确诊病例较多的省市大部分都是在湖北周围,很大原因是由于携带病毒的流动人口造成的,所以控制疫情的有效手段是在家隔离,同时也可以推断在新疆和甘肃等西北地区疫情相对缓和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年全球超级计算机500强名单公布,中国超级计算机“神威·太湖之光”和“天河二号”携手夺得前两名.已知“神威·太湖之光”的浮点运算速度是“天河二号”的2.74倍.这两种超级计算机分别进行100亿亿次浮点运算,“神威·太湖之光”的运算时间比“天河二号”少18.75秒,求这两种超级计算机的浮点运算速度.设“天河二号”的浮点运算速度为
 亿亿次/秒,依题意,可列方程为___________.
亿亿次/秒,依题意,可列方程为___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
相关试题

