【题目】如图,有小岛A和小岛B,轮船以45km/h的速度由C向B航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈2.45)
≈2.45)

参考答案:
【答案】小岛A与小岛B之间的距离是100km.
【解析】试题分析:
先过点C作CP⊥AB于P,根据已知条件求出∠PCB=∠PBC=45°,∠CAP=60°,再根据轮船的速度和航行的时间求出BC的值,在Rt△PCB中,根据勾股定理求出BP=CP的值,再根据特殊角的三角函数值求出AP的值,最后根据AB=AP+PB,即可求出答案.
试题解析:
解:过点C作CP⊥AB于P,
∵∠BCF=45°,∠ACE=60°,AB∥EF,
∴∠PCB=∠PBC=45°,∠CAP=60°,
∵轮船的速度是45km/h,轮船航行2小时,
∴BC=90,
∵BC2=BP2+CP2,
∴BP=CP=45![]() ,
,
∵∠CAP=60°,
∴tan60°=![]() =
=![]() ,
,
∴AP=15![]() ,
,
∴AB=AP+PB=15![]() +45
+45![]() =15×2.45+45×1.41≈100(km).
=15×2.45+45×1.41≈100(km).
答:小岛A与小岛B之间的距离是100km.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
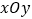 中,直线
中,直线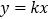 与双曲线
与双曲线 相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )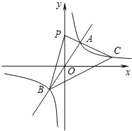
A. (3,1) B. (3,2) C. (6,2) D. (6,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)把数轴补充完整.
(2)在数轴上表示下列各数:3
 ,﹣4,﹣(﹣1.5),﹣|﹣2|.
,﹣4,﹣(﹣1.5),﹣|﹣2|.(3)用“<”连接起来._____________
(4)﹣|﹣2|与﹣4之间的距离是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点
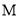 (
(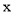 ,0)是
,0)是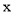 轴上的一个动点,它与原点的距离的2倍为
轴上的一个动点,它与原点的距离的2倍为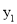 .
.(1)求
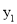 关于
关于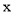 的函数解析式,并在所给网格中画出这个函数图象;
的函数解析式,并在所给网格中画出这个函数图象;(2)若反比例函数
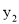 =
=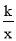 的图象与函数
的图象与函数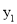 的图象相交于点
的图象相交于点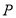 ,且点
,且点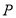 的纵坐标为2.
的纵坐标为2.①求k的值;
②结合图象,当
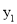 >
>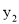 时,写出
时,写出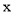 的取值范围.
的取值范围.(3)过原点的一条直线交
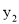 =
=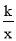 (
(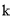 >0)于
>0)于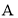 、
、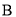 两点(点
两点(点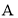 在点
在点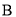 的右侧),分别过点
的右侧),分别过点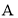 、
、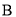 作
作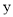 轴和
轴和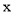 轴的平行线,两平行线交于点
轴的平行线,两平行线交于点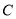 ,则△
,则△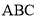 的面积是 .
的面积是 .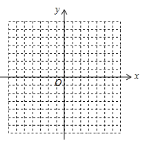
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为______.
(3)若x表示一个数,数轴上表示x和﹣5的两点之间的距离是____;(用含x的式子表示)
(4)若x表示一个数,|x+1|+|x﹣2|的最小值是______,相应的x的取值范围_______.
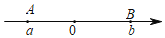
-
科目: 来源: 题型:
查看答案和解析>>【题目】有五张正面分别标有数字—2、—1、0、1、2的不透明卡片,它们除数字不同外其余全部相同,现将它们背面向上,洗匀后从中任取一张,将卡片上的数字记为
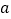 ,则
,则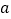 使关于
使关于 的一元一次方程
的一元一次方程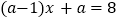 有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
有整数解,且方程的整数解能与2,6组成三角形的概率是____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,某班同学用天平和一些物品(如图)探究了等式的基本性质.该班科技创新小组的同学提出问题:仅用一架天平和一个10克的砝码能否测量出乒乓球和一次性纸杯的质量?科技创新小组的同学找来足够多的乒乓球和某种一次性纸杯(假设每个乒乓球的质量相同,每个纸杯的质量也相同),经过多次试验得到以下记录:

记录
天平左边
天平右边
状态
记录一
6个乒乓球,
1个10克的砝码
14个一次性纸杯
平衡
记录二
8个乒乓球
7个一次性纸杯,
1个10克的砝码
平衡
请算一算,一个乒乓球的质量是多少克?一个这种一次性纸杯的质量是多少克?
解:(1)设一个乒乓球的质量是
 克,则一个这种一次性纸杯的质量是______克;(用含
克,则一个这种一次性纸杯的质量是______克;(用含 的代数式表示)
的代数式表示)(2)列一元一次方程求一个乒乓球的质量,并求出一个这种一次性纸杯的质量.
相关试题

