【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
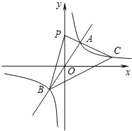
与双曲线![]() 相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
相交于A、B两点,C是第一象限内的双曲线上与点A不重合的一点,连接CA并延长交y轴于点P,连接BP,BC。若点A坐标 (2,3),△PBC的面积是24,则点C坐标为( )
A. (3,1) B. (3,2) C. (6,2) D. (6,1)
参考答案:
【答案】D
【解析】分析:根据待定系数法求得k、m的值,设设C点坐标为(a,![]() ),根据反比例函数与一次函数的交点问题解方程组
),根据反比例函数与一次函数的交点问题解方程组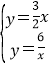 可得到A点坐标为(2,3),B点坐标为(-2,-3),再利用待定系数法确定直线BC的解析式为y=
可得到A点坐标为(2,3),B点坐标为(-2,-3),再利用待定系数法确定直线BC的解析式为y=![]() ,直线AC的解析式为y=-
,直线AC的解析式为y=-![]() ,于是利用y轴上点的坐标特征得到D点坐标为(0,
,于是利用y轴上点的坐标特征得到D点坐标为(0,![]() -3),P点坐标为(0,
-3),P点坐标为(0,![]() +3),然后利用S△PBC=S△PBD+S△CPD得到关于a的方程,求出a的值即可得到C点坐标.
+3),然后利用S△PBC=S△PBD+S△CPD得到关于a的方程,求出a的值即可得到C点坐标.
详解:∵点A的坐标为(2,3),
∴k=![]() ,m=6,
,m=6,
设BC交y轴于D,如图,设C点坐标为(a,![]() )
)
解方程组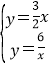 得
得![]() 或
或![]() ,
,
∴A点坐标为(2,3),B点坐标为(-2,-3),
设直线BC的解析式为y=k′x+b,
把B(-2,-3)、C(a,![]() )代入得
)代入得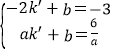 ,
,
解得 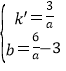 ,
,
∴直线BC的解析式为y=![]() ,
,
当x=0时,y=![]() =
=![]() ,
,
∴D点坐标为(0,![]() )
)
设直线AC的解析式为y=m′x+n,
把A(2,3)、C(a,![]() )代入得
)代入得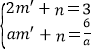 ,
,
解得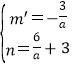 ,
,
∴直线AC的解析式为y=-![]() ,
,
当x=0时,y=-![]() =
=![]() ,
,
∴P点坐标为(0,![]() )
)
∵S△PBC=S△PBD+S△CPD,
∴![]() ×2×6+
×2×6+![]() ×a×6=24,解得a=6,
×a×6=24,解得a=6,
∴C点坐标为(6,1).
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总数为________人.家长表示“不赞同”的人数为________人;
(2)请在图①中把条形统计图补充完整;
(3)从这次接受调查的家长中随机抽查一个,恰好是“赞同”的家长的概率是________;
(4)求图②中表示家长“无所谓”的扇形圆心角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)﹣2+(﹣7)+8.
(2)25﹣13﹣4﹣25.
(3)
 .
.(4)(﹣2.4)﹣(﹣4.5)+|﹣2.4|+(﹣0.5).
(5)(
 )×(﹣36).
)×(﹣36).(6)
 .
.(7)
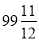 ×(﹣12).
×(﹣12).(8)13×(﹣
 )+(﹣13)×
)+(﹣13)× +13×
+13× .
.(9)﹣12018+
 .
.(10)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )
A. ∠AOC=∠BOC B. ∠AOB=2∠BOC
C. ∠AOC=
 ∠AOB D. ∠AOC+∠BOC=∠AOB
∠AOB D. ∠AOC+∠BOC=∠AOB -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)把数轴补充完整.
(2)在数轴上表示下列各数:3
 ,﹣4,﹣(﹣1.5),﹣|﹣2|.
,﹣4,﹣(﹣1.5),﹣|﹣2|.(3)用“<”连接起来._____________
(4)﹣|﹣2|与﹣4之间的距离是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点
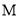 (
(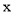 ,0)是
,0)是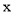 轴上的一个动点,它与原点的距离的2倍为
轴上的一个动点,它与原点的距离的2倍为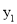 .
.(1)求
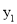 关于
关于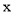 的函数解析式,并在所给网格中画出这个函数图象;
的函数解析式,并在所给网格中画出这个函数图象;(2)若反比例函数
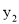 =
=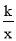 的图象与函数
的图象与函数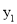 的图象相交于点
的图象相交于点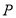 ,且点
,且点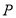 的纵坐标为2.
的纵坐标为2.①求k的值;
②结合图象,当
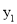 >
>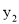 时,写出
时,写出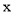 的取值范围.
的取值范围.(3)过原点的一条直线交
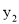 =
=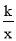 (
(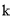 >0)于
>0)于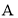 、
、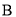 两点(点
两点(点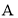 在点
在点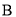 的右侧),分别过点
的右侧),分别过点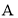 、
、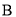 作
作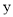 轴和
轴和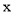 轴的平行线,两平行线交于点
轴的平行线,两平行线交于点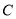 ,则△
,则△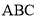 的面积是 .
的面积是 .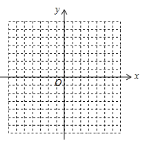
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有小岛A和小岛B,轮船以45km/h的速度由C向B航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据:
 ≈1.41,
≈1.41,  ≈2.45)
≈2.45)
相关试题

