【题目】有五张正面分别标有数字—2、—1、0、1、2的不透明卡片,它们除数字不同外其余全部相同,现将它们背面向上,洗匀后从中任取一张,将卡片上的数字记为![]() ,则
,则![]() 使关于
使关于![]() 的一元一次方程
的一元一次方程![]() 有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
有整数解,且方程的整数解能与2,6组成三角形的概率是____________.
参考答案:
【答案】![]()
【解析】分析:分别把5个数代入方程,然后解方程可确定![]() 的一元一次方程
的一元一次方程![]() 有整数解的a的值,再利用概率公式求解.
有整数解的a的值,再利用概率公式求解.
详解:当a=-2时,方程![]() 的解为
的解为![]() ;
;
当a=-1时,方程![]() 的解为
的解为![]() ;
;
当a=0时,方程![]() 的解为x=-8;
的解为x=-8;
当a=1时,方程无解;
当a=2时,方程![]() 的解为x=6,
的解为x=6,
所以从中任取一张,将该卡片上的数字记为a,关于![]() 的一元一次方程
的一元一次方程![]() 有整数解,且方程的整数解能与2,6组成三角形的概率是
有整数解,且方程的整数解能与2,6组成三角形的概率是![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点
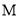 (
(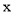 ,0)是
,0)是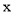 轴上的一个动点,它与原点的距离的2倍为
轴上的一个动点,它与原点的距离的2倍为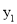 .
.(1)求
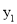 关于
关于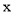 的函数解析式,并在所给网格中画出这个函数图象;
的函数解析式,并在所给网格中画出这个函数图象;(2)若反比例函数
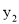 =
=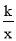 的图象与函数
的图象与函数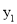 的图象相交于点
的图象相交于点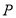 ,且点
,且点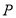 的纵坐标为2.
的纵坐标为2.①求k的值;
②结合图象,当
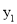 >
>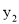 时,写出
时,写出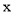 的取值范围.
的取值范围.(3)过原点的一条直线交
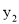 =
=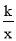 (
(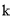 >0)于
>0)于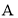 、
、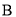 两点(点
两点(点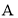 在点
在点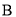 的右侧),分别过点
的右侧),分别过点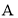 、
、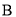 作
作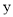 轴和
轴和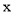 轴的平行线,两平行线交于点
轴的平行线,两平行线交于点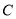 ,则△
,则△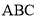 的面积是 .
的面积是 .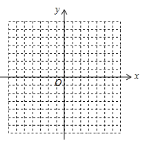
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有小岛A和小岛B,轮船以45km/h的速度由C向B航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据:
 ≈1.41,
≈1.41,  ≈2.45)
≈2.45)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
(1)数轴上表示2和10两点之间的距离是_______.
(2)数轴上一个点到表示2的点的距离为5.2,这个点表示的数为______.
(3)若x表示一个数,数轴上表示x和﹣5的两点之间的距离是____;(用含x的式子表示)
(4)若x表示一个数,|x+1|+|x﹣2|的最小值是______,相应的x的取值范围_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,某班同学用天平和一些物品(如图)探究了等式的基本性质.该班科技创新小组的同学提出问题:仅用一架天平和一个10克的砝码能否测量出乒乓球和一次性纸杯的质量?科技创新小组的同学找来足够多的乒乓球和某种一次性纸杯(假设每个乒乓球的质量相同,每个纸杯的质量也相同),经过多次试验得到以下记录:

记录
天平左边
天平右边
状态
记录一
6个乒乓球,
1个10克的砝码
14个一次性纸杯
平衡
记录二
8个乒乓球
7个一次性纸杯,
1个10克的砝码
平衡
请算一算,一个乒乓球的质量是多少克?一个这种一次性纸杯的质量是多少克?
解:(1)设一个乒乓球的质量是
 克,则一个这种一次性纸杯的质量是______克;(用含
克,则一个这种一次性纸杯的质量是______克;(用含 的代数式表示)
的代数式表示)(2)列一元一次方程求一个乒乓球的质量,并求出一个这种一次性纸杯的质量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直线
 上一点
上一点 为端点作射线
为端点作射线 ,使
,使 ,在同一个平面内将一个直角三角板的直角顶点放在点
,在同一个平面内将一个直角三角板的直角顶点放在点 处.(注:
处.(注: )
)(1)如图1,如果直角三角板
 的一边
的一边 放在射线
放在射线 上,那么
上,那么 的度数为______;
的度数为______;
(2)如图2,将直角三角板
 绕点
绕点 按顺时针方向转动到某个位置,如果
按顺时针方向转动到某个位置,如果 恰好平分
恰好平分 ,求
,求 的度数;
的度数;
(3)如图3,将直角三角板
 绕点
绕点 任意转动,如果
任意转动,如果 始终在
始终在 的内部,请直接用等式表示
的内部,请直接用等式表示 和
和 之间的数量关系.
之间的数量关系.
相关试题

