搜索
【题目】小明和小刚相约周末到净月潭国家森林公园去徒步，小明和小刚的家分别距离公园1600米和2800米，两人分别从家中同时出发，小明骑自行车，小刚乘公交车，已知公交车的平均速度是骑自行车速度的3.5倍，结果小刚比小明提前4min到达公园，求小刚乘公交车的平均速度．
参考答案：
【答案】小刚乘公交车的平均速度为700米/分钟．
【解析】
设小明骑自行车的平均速度为x米/分钟，则小刚乘公交车的平均速度为3.5x米/分钟，根据时间=路程÷速度结合小刚比小明提前4min到达公园，即可得出关于x的分式方程，解之经检验后即可得出结论．
设小明骑自行车的平均速度为x米/分钟，则小刚乘公交车的平均速度为3.5x米/分钟，
依题意，得：
=4，
解得：x＝200，
经检验，x＝200是原方程的解，且符合题意，
∴3.5x＝700．
答：小刚乘公交车的平均速度为700米/分钟．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店准备购进
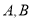两种商品，
种商品毎件的进价比
种商品每件的进价多20元，用3000元购进种商品和用1800元购进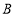种商品的数量相同．商店将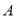种商品每件的售价定为80元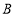，种商品每件的售价定为45元．（1）
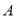种商品每件的进价和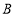种商品每件的进价各是多少元？（2）商店计划用不超过1560元的资金购进
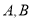两种商品共40件，其中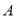种商品的数量不低于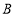种商品数量的一半，该商店有几种进货方案？（3）端午节期间，商店开展优惠促销活动，决定对每件
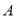种商品售价优惠
（
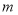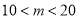）元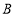，种商品售价不变，在（2）条件下，请设计出销售这40件商品获得总利润最大的进货方案． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知A（a，b），B（2，2），且|a-b+8|+
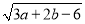=0．（1）求点A的坐标；
（2）过点A作AC⊥x轴于点C，连接BC，AB，延长AB交x轴于点D，设AB交y轴于点E，那么OD与OE是否相等？请说明理由．
（3）在x轴上是否存在点P，使S△OBP=S△BCD？若存在，请求出P点坐标，若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】正方形ABCD的边长为6cm，点E，M分别是线段BD，AD上的动点，连接AE并延长，交边BC于F，过M作MN⊥AF，垂足为H，交边AB于点N.
(1)如图①，若点M与点D重合，求证：AF＝MN；
(2)如图②，若点M从点D出发，以1cm/s的速度沿DA向点A运动，同时点E从点B出发，以
cm/s的速度沿BD向点D运动，运动时间为ts.①设BF＝ycm，求y关于t的函数表达式；
②当BN＝2AN时，连接FN，求FN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小东同学根据函数的学习经验，对函数y
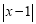
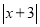进行了探究，下面是他的探究过程：（1）已知x＝-3时
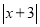0；x＝1 时 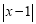0，化简：①当x＜-3时，y＝ ；
②当-3≤x≤1时，y＝ ；
③当x＞1时，y＝ ．
（2）在平面直角坐标系中画出y＝|x﹣1|+|x+3|的图象，根据图象，写出该函数的一条性质： ；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠1＝∠2，G为AD的中点，BG的延长线交AC于点E，F为AB上的一点，CF与AD垂直，交AD于点H，则下面判断正确的有（ ）
①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；
③CH是△ACD的边AD上的高；④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知矩形ABCD的两条对角线相交于点O，过点 A作AG⊥BD分别交BD、BC于点G、E．
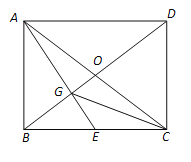
（1）求证：BE2=EGEA；
（2）连接CG，若BE=CE，求证：∠ECG=∠EAC．
相关试题
