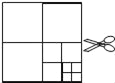
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2017个小正方形,则需要操作的次数是( )
A. 672 B. 671 C. 670 D. 674
参考答案:
【答案】A
【解析】
由题意可知:第一次操作后有正方形4个;第二次操作后正方形的个数为:4﹣1+4=2×4﹣1,第三次操作后正方形的个数有:4﹣1+4﹣1+4=3×4﹣2,第四次操作后正方形的个数有: 4﹣1+4﹣1+4﹣1+4=4×4﹣3,…第n次操作后正方形的个数有:4n﹣(n﹣1)=3n+1,令3n+1=2017,解方程即可求解.
根据题意可得:第n次操作后正方形的个数有(3n+1)个,
设第n次操作后正方形的个数有2017个,
则:3n+1=2017,
解得,n=672,
即:若要得到2017个小正方形,需要操作的次数是672次.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg)
120
130
…
180
每天销量y(kg)
100
95
…
70
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

-
科目: 来源: 题型:
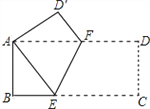
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图形都是由相同的正方形按一定的规律组成,其中:第(1)个图形中的正方形有2个,第(2)个图形中的正方形有5个,第(3)个图形中的正方形有9个,…,按此规律,则第7个图形中的正方形的个数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,航空母舰始终以40千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行4个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.

(1)判断四边形CEGF的形状,并证明你的结论;
(2)若AB=3,BC=9,求线段CE的取值范围.
相关试题

