【题目】如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,求直尺的宽度.
参考答案:
【答案】解:作 OF⊥DE 于点F,连接OD,
∵ OF⊥DE ,
∴ DF=EF=![]() DE=4 ,
DE=4 ,
∵ OD=OC=5 ,
∴ OF=![]() =
=![]() =3(cm),
=3(cm),
∴直尺的宽度为3cm.
【解析】作 OF⊥DE 于点F,连接OD,根据垂径定理得出DF=EF=![]() DE=4 ,在Rt△DOF中,由勾股定理求出OF的长,即直尺的宽度.
DE=4 ,在Rt△DOF中,由勾股定理求出OF的长,即直尺的宽度.
【考点精析】通过灵活运用勾股定理的概念和垂径定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c,当x取1时,函数有最大值为3,且函数的图象经过点(-2,0)。
(1)求这个二次函数的解析式;
(2)根据图象直接写出函数值y大于零时x的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1):
(1)请画出△ABC沿
 轴向右平移3个单位长度,再沿
轴向右平移3个单位长度,再沿 轴向上平移2个单位长度后的
轴向上平移2个单位长度后的 (其中
(其中 分别是A、B、C的对应点,不写画法);
分别是A、B、C的对应点,不写画法);(2)直接写出
 三点的坐标;
三点的坐标;(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】常用的分解因式的方法有提取公因式法、公式法,但有更多的多项式只用上述方法就无法分解,如
 ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了,过程为: ,这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.
,这种分解因式的方法叫分组分解法,利用这种方法解决下列问题.(1)分解因式:
 ;
;(2)△ABC三边a、b、c满足
 ,判断△ABC的形状.
,判断△ABC的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
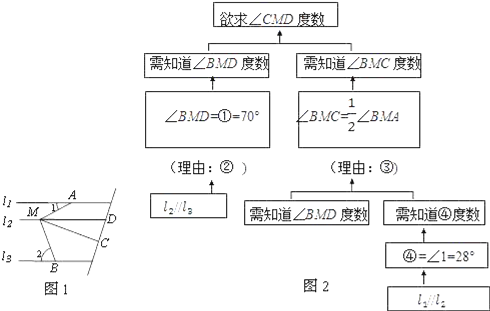
请问小坚的提示中①是∠ ,④是∠ .
理由②是: ;
理由③是: ;
∠CMD的度数是 °.
相关试题

