【题目】小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
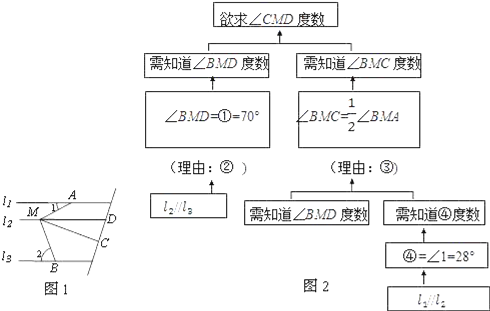
请问小坚的提示中①是∠ ,④是∠ .
理由②是: ;
理由③是: ;
∠CMD的度数是 °.
参考答案:
【答案】2;AMD;两直线平行,内错角相等;角平分线定义;21
【解析】试题分析:根据两直线平行,内错角相等可得∠BMD=∠2=70°,∠1=∠AMD=28°,即可得∠AMB=∠AMD+∠BMD=98°,根据角平分线的定义可得∠BMC=![]() ∠AMB=49,即可得∠CMD=∠BMD-∠BMC=21°.
∠AMB=49,即可得∠CMD=∠BMD-∠BMC=21°.
试题解析:
∵l1∥l2∥l3,
∴∠1=∠AMD=28°,∠2=∠DMB=70°(两直线平行,内错角相等),
∴∠AMB=28°+70°=98°,
∵MC平分∠AMB,
∴∠BMC=![]() ∠AMB=98°×
∠AMB=98°×![]() =49°(角平分线定义),
=49°(角平分线定义),
∴∠DMC=70°﹣49°=21°,
故答案为:2;AMD;两直线平行,内错角相等;角平分线定义;21.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )

A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:
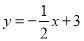 交y轴于点A,交x轴于点B,过点E(2,0)作x轴的垂线EF交AB于点D,点P是垂线EF上一点,且S△ADP=2,以PB为边在第一象限作等腰Rt△BPC,则点C的坐标为_________.
交y轴于点A,交x轴于点B,过点E(2,0)作x轴的垂线EF交AB于点D,点P是垂线EF上一点,且S△ADP=2,以PB为边在第一象限作等腰Rt△BPC,则点C的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:① ∠AEB的度数为_______;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为 ;
(4)试在y轴上找一点Q(在图中标出来),使得点Q到B2、C2两点的距离之和最小,并求出QB2+QC2的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列线段是否成比例,若是,请写出比例式.
(1)a=3 m,b=5 m,c=4.5 cm,d=7.5 cm;
____________________
(2)a=7 cm,b=4 cm,c=d=2
 cm;
cm;____________________
(3)a=1.1 cm,b=2.2 cm,c=3.3 cm,d=5.5 cm.
____________________
相关试题

