【题目】(1)问题发现
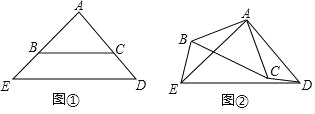
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究
如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0<α<360),请判断线段BE与线段CD的数量关系,并说明理由.
参考答案:
【答案】(1)BE=CD;(2)BE=CD;证明见解析.
【解析】
(1)根据等腰直角三角形的性质可得AB=AC,AE=AD,再根据等量关系可得线段BE与线段CD的关系;
(2)根据等腰直角三角形的性质可得AB=AC,AE=AD,根据旋转的性质可得∠BAE=∠CAD,根据SAS可证△BAE≌△CAD,根据全等三角形的性质即可求解;
解:(1)BE=CD,理由如下;
∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
∴AE﹣AB=AD﹣AC,
∴BE=CD;
故答案为:BE=CD.
(2)∵△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
由旋转的性质得,∠BAE=∠CAD,
在△BAE与△CAD中,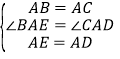 ,
,
∴△BAE≌△CAD(SAS)
∴BE=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧
 (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( ) 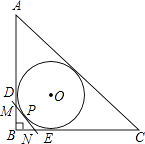
A.r
B. ?r
?r
C.2r
D. ?r
?r -
科目: 来源: 题型:
查看答案和解析>>【题目】以直线AB上一点O为端点作射线OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=
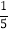 ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
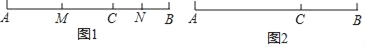
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB:BC=3:4,AC=5,点P从点A出发,以每秒1个单位的速度,沿△ABC边A→B→C→A的方向运动,运动时间为t秒.
(1)求AB与BC的长;
(2)在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.

-
科目: 来源: 题型:
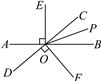
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,EO⊥AB于点O,FO⊥CD于点O.
(1)图中除直角外,还有其他相等的角,请写出两对:①______________;②______________.
(2)如果∠AOD=40°,那么:
①根据__________,可得∠BOC=________;
②求∠POF的度数.
相关试题

