搜索
【题目】用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②三棱锥；③圆柱；④圆锥 _____（写出所有正确结果的序号）．
参考答案：
【答案】①②④
【解析】
当截面的角度和方向不同时，圆柱体的截面无论什么方向截取圆柱都不会截得三角形．
①当平面经过正方体的三个顶点时，所得到的截面为三角形.
②当平面平行于三棱锥的任意面时，得到的截面都是三角形.
③用平面截圆柱时，可以得到圆，椭圆或长方形，不能得到三角形截面.
④当平面沿着母线截圆锥时，可以得到三角形截面.
故答案为:①②④.
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：“半角问题”：
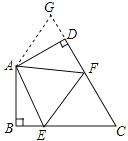
（1）如图：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段EF，BE，FD之间的数量关系．
小明同学探究此“半角问题”的方法是：延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；（直接写结论，不需证明）
探索延伸：当聪明的你遇到下面的问题该如何解决呢？
（2）若将（1）中“∠BAD=120°，∠EAF=60°”换为∠EAF=
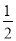∠BAD．其它条件不变。如图1，试问线段EF、BE、FD具有怎样的数量关系，并证明．（3）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=
∠BAD，请直接写出线段EF、BE、FD它们之间的数量关系．（不需要证明）（4）如图3，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=
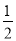∠BAD，试问线段EF、BE、FD具有怎样的数量关系，并证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列所述物体中，是球体的是（ ）
A. 铅笔 B. 打足气的自行车内胎 C. 乒乓球 D. 电视机
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下列图形中，不属于中心对称图形的是（ ）
A.等边三角形B.平行四边形C.矩形D.正六边形
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下列命题中，是假命题的是（ ）
A. 有一个角是直角的平行四边形是矩形 B. 一组邻边相等的矩形是正方形
C. 一组对边平行且相等的四边形是平行四边形 D. 有两组邻边相等的四边形是菱形
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.有一个角是直角的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.对角线相等且互相垂直的四边形是正方形
D.四条边都相等的四边形是正方形
-
科目： 来源： 题型：
查看答案和解析>>【题目】7m2-21m的公因式是________；0.12530×831=________．
相关试题
