搜索
【题目】正方形
、
、
…按如图所示的方式放置.点
、
、
…和点
、
、
…别在直线
和
轴上，则点
的坐标是（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】B
【解析】
利用一次函数图象上点的坐标特征及正方形的性质可得出点
的坐标，根据点的坐标的变化可找出变化规律“点
的坐标为
（n为正整数）”，再代入n=2019即可得出的坐标，然后再将其横坐标减去纵坐标得到
的横坐标，和的纵坐标相同．
解：当
时，
，
∴点A1的坐标为（0，1）．
∵四边形A1B1C1O为正方形，
∴点B1的坐标为（1，1），点C1的坐标为（1，0）．
当
时，
，
∴点A2的坐标为（1，2）．
∵A2B2C2C1为正方形，
∴点B2的坐标为（3，2），点C2的坐标为（3，0）．
同理，可知：点B3的坐标为（7，4），点B4的坐标为（15，8），点B5的坐标为（31，16），…，
∴点的坐标为
（n为正整数），
∴点
的坐标为
，
∴点
的坐标为
，即为
．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：关于 x 的方程 2x2+kx﹣1=0．
（1）求证：方程有两个不相等的实数根；
（2）若方程的一个根是﹣1，求另一个根及 k 值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)已知
，求
的最小值.爱思考的小思想到了一种方法：先用
表示
得：
_____；再把
代入得到：
______；再利用配方法得到：
(
_____)
+______；根据完全平方式的非负性，就得到了
的最小值是______.请你补充完成小思的解答过程：
(2)根据小思的方法，请你求出：当
时，求出
的最小值.(3)但是假如变成
，求
的最小值的时候小思的方法就不好用了，因此喜欢面对挑战的小喻同学想到了一种叫增量代换法：设
，
，
，
，∵
，∴
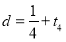，则
，
，
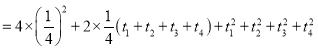.故
的最小值是
.参考小喻的方法，当
时，求出
的最小值. -
科目： 来源： 题型：
查看答案和解析>>【题目】游泳是一项深受青少年喜爱的体育活动，学校为了加强学生的安全意识，组织学生观看了纪实片“孩子，请不要私自下水”，并于观看后在本校的2000名学生中作了抽样调查．请根据下面两个不完整的统计图回答以下问题：
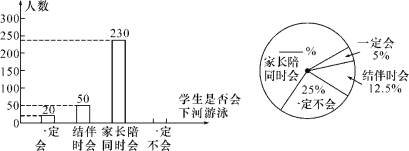
(1)这次抽样调查中，共调查了__ __名学生；
(2)补全两个统计图；
(3)根据抽样调查的结果，估算该校2000名学生中大约有多少人“一定会下河游泳”？
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙二人从学校出发去科技馆，甲步行一段时间后，乙骑自行车沿相同路线行进，两人均匀速前行，他们的路程差S（米）与甲出发时间t（分）之间的函数关系如图所示．下列说法：①乙先到达科技馆；②乙的速度是甲速度的2.5倍；③b＝480；④a＝24．其中，正确的是 ______（填序号）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知 三角形ABC各顶点在格点上
（1）直接写出三角形ABC的三个顶点的坐标
A B C ；
（2）画出三角形ABC关于y轴对称的三角形A′B′C′.
（3）求三角形ABC的面积；
（4）直接与出A′C′与y轴交点的坐标 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地长途汽车站规定前来乘车的旅客可以免费随身携带一定质量的行李，如果行李质量超过规定，则应交纳行李费，行李费用y（元）与行李质量x（千克）之间的关系可以用如图所示的图象表示，请观察图象回答下列问题：
（1）旅客最多能免费携带多少千克的行李？
（2）求行李费用y（元）与行李质量x（千克）之间的函数关系式；
（3）一位旅客随身携带了60千克的行李，他应交纳行李费多少元？
（4）另一位旅客交纳了120元行李费，他携带的行李重多少千克？
相关试题
