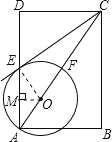
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.

参考答案:
【答案】(1)直线CE与⊙O相切(2)![]()
【解析】试题分析:(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;
(2)在直角三角形ABC中,根据三角函数的定义可以求得AB=![]() ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC=![]() ,同理知DE=1;在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即(
,同理知DE=1;在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2,即(![]() -r) 2=r2+3,从而易得r的值;
-r) 2=r2+3,从而易得r的值;
试题解析:(1)直线CE与⊙O相切
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AEO+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切.
(2)∵tan∠ACB=![]() ,BC=2,
,BC=2,
∴AB=BCtan∠ACB=![]() ,
,
∴AC=![]() ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB=![]() ,
,
∴DE=DCtan∠DCE=1;
在Rt△CDE中,CE=![]() ,
,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即(![]() -r) 2=r2+3
-r) 2=r2+3
解得:r=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程x2-ax+a-1=0有两个相等的实数根,那么a的值等于______
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:3(x+2)>﹣1﹣2(x﹣1),并把解集在数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+2|=0,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
(1)2(a﹣1)﹣(2a﹣3)+3
(2)2(x2y+3xy2)﹣3(2xy2﹣4x2y) -
科目: 来源: 题型:
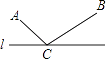
查看答案和解析>>【题目】如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角 -
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见表:
一户居民一个月用电量的范围
电费价格(单位:元/度)
不超过200度
a
超过200度的部分
b
已知4月份,该市居民甲用电250度,交电费130元;居民乙用电400度,交电费220元.
(1)求出表中a和b的值;
(2)实行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度不超过0.56元?
相关试题

