【题目】某中学采用随机的方式对学生掌握安全知识的情况进行测评,并按成绩高低分成优、良、中、差四个等级进行统计,绘制了下面两幅尚不完整的统计图.请根据有关信息解答: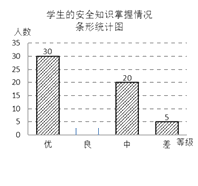

(1)接受测评的学生共有人,扇形统计图中“优”部分所对应扇形的圆心角为°,并补全条形统计图;
(2)若该校共有学生1200人,请估计该校对安全知识达到“良”程度的人数;
(3)测评成绩前五名的学生恰好3个女生和2个男生,现从中随机抽取2人参加市安全知识竞赛,请用树状图或列表法求出抽到1个男生和1个女生的概率.
参考答案:
【答案】
(1)80,135
(2)解:该校对安全知识达到“良”程度的人数为:1200×![]() =375(人),
=375(人),
答:估计该校对安全知识达到“良”程度的人数为375人.
(3)解:根据题意画出树状图如下: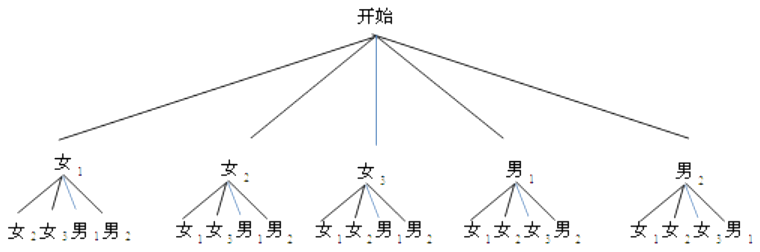
∴所有等可能的结果为20种,其中抽到一男一女的等可能结果有12种,
∴抽到1个男生和1个女生的概率为:![]() =
=![]() .
.
【解析】解:(1)依题可得:接受测评的学生人数为:20÷25%=80(人),
∴“优”程度所对应扇形的圆心角为:![]() ×360°=135°,
×360°=135°,
∴达到“良”程度的人数为:80-30-20-5=25(人),
补全条形统计图如下: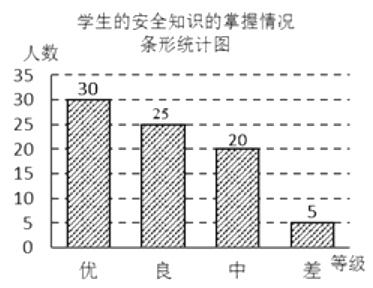
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式及其展开式
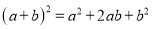
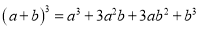
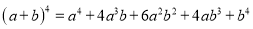

······
请你猜想
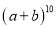 的展开式第三项的系数是( )
的展开式第三项的系数是( )A.
 B.
B.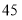 C.
C.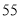 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=
 ,y=
,y=
(1)求x2+xy+y2.
(2)若x的小数部分为a,y的整数部分为b,求ax+by的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①计算:(-1)2+
 -
- 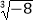 -︱-5︱
-︱-5︱
②用适当的方法解方程:x2=2x+35. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机动车辆出发前油箱中有油
 升,行驶若干小时后,在途中加油站加油若干.油箱中余油量
升,行驶若干小时后,在途中加油站加油若干.油箱中余油量 (升)与行驶时间
(升)与行驶时间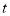 (时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(1)机动车辆行驶了 小时后加油,中途加油________升.
(2)加油后油箱中的油最多可行驶多少小时?
(3)若加油站距目的地还有
 公里,机动车每小时走
公里,机动车每小时走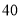 公里,油箱中的油能否使车到达目的地?
公里,油箱中的油能否使车到达目的地? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系上,已知点A(8,4),AB⊥y轴于B,AC⊥x轴于C,直线y=x交AB于D.
(1)直接写出B、C、D三点坐标;
(2)若E为OD延长线上一动点,记点E横坐标为a,△BCE的面积为S,求S与a的关系式;
(3)当S=20时,过点E作EF⊥AB于F,G、H分别为AC、CB上动点,求FG+GH的最小值.

相关试题

