【题目】①计算:(-1)2+ ![]() -
- ![]() -︱-5︱
-︱-5︱
②用适当的方法解方程:x2=2x+35.
参考答案:
【答案】【解答】解:①原式=1+2-(-2)-5,
=0.
②∵x2=2x+35,
∴x2-2x-35=0,
∴(x-7)(x+5)=0,
∴x1=7,x2=-5,
∴原方程的根为:x1=7,x2=-5.
【解析】①根据有理数的乘方,二次根式,立方根,绝对值的性质即可得出答案.
②用十字相乘法因式分解即可求出原方程的根.
【考点精析】关于本题考查的因式分解法和绝对值,需要了解已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式及其展开式
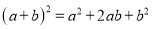
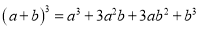
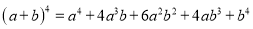

······
请你猜想
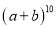 的展开式第三项的系数是( )
的展开式第三项的系数是( )A.
 B.
B.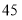 C.
C.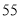 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=
 ,y=
,y=
(1)求x2+xy+y2.
(2)若x的小数部分为a,y的整数部分为b,求ax+by的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学采用随机的方式对学生掌握安全知识的情况进行测评,并按成绩高低分成优、良、中、差四个等级进行统计,绘制了下面两幅尚不完整的统计图.请根据有关信息解答:
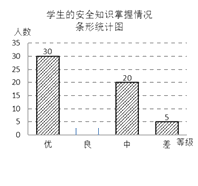

(1)接受测评的学生共有人,扇形统计图中“优”部分所对应扇形的圆心角为°,并补全条形统计图;
(2)若该校共有学生1200人,请估计该校对安全知识达到“良”程度的人数;
(3)测评成绩前五名的学生恰好3个女生和2个男生,现从中随机抽取2人参加市安全知识竞赛,请用树状图或列表法求出抽到1个男生和1个女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机动车辆出发前油箱中有油
 升,行驶若干小时后,在途中加油站加油若干.油箱中余油量
升,行驶若干小时后,在途中加油站加油若干.油箱中余油量 (升)与行驶时间
(升)与行驶时间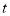 (时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(时)之间的关系如图,请根据图中给出的信息,解决下列问题.
(1)机动车辆行驶了 小时后加油,中途加油________升.
(2)加油后油箱中的油最多可行驶多少小时?
(3)若加油站距目的地还有
 公里,机动车每小时走
公里,机动车每小时走 公里,油箱中的油能否使车到达目的地?
公里,油箱中的油能否使车到达目的地?
相关试题

