【题目】某社区决定购置一批共享单车,经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需1600元.
(1)求男式单车和女式单车每辆分别是多少元?
(2)该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过5000元,问该社区有几种购置方案?怎样的购置才能使所需总费用最低?最低费用是多少?
参考答案:
【答案】(1)男式单车200元/辆,女式单车150元/辆;(2)见解析.
【解析】
(1)设男式单车x元/辆,女式单车y元/辆,根据“购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需1600元”列方程组求解可得;
(2)设购置女式单车m辆,则购置男式单车(m+4)辆,根据“两种单车至少需要22辆、购置两种单车的费用不超过5000元”列不等式组求解,得出m的范围,即可确定购置方案;再列出购置总费用关于m的函数解析式,利用一次函数性质结合m的范围可得其最值情况.
解:(1)设男式单车x元/辆,女式单车y元/辆,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:男式单车200元/辆,女式单车150元/辆;
(2)设购置女式单车m辆,则购置男式单车(m+4)辆,
根据题意,得:![]() ,
,
解得:9≤m≤12,
∵m为整数,
∴m的值可以是9、10、11、12,即该社区有四种购置方案;
设购置总费用为W,
则W=200(m+4)+150m=350m+800,
∵W随m的增大而增大,
∴当m=9时,W取得最小值,最小值为3950,
答:该社区共有4种购置方案,其中购置男式单车13辆、女式单车9辆时所需总费用最低,最低费用为3950元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程
 =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,童威随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
(1)本次被调查的学生人数为 ,扇形统计图中“跑步”所对的圆心角为 度.
(2)补全条形统计图;
(3)该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
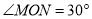 ,点
,点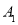 、
、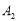 、
、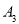 、…在射线ON上,点
、…在射线ON上,点 、
、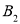 、
、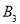 、…在射线OM上,
、…在射线OM上, 、
、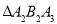 、
、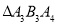 …均为等边三角形,若
…均为等边三角形,若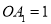 ,则
,则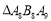 的边长为( )
的边长为( )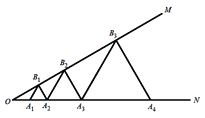
A.16B.64C.128D.256
-
科目: 来源: 题型:
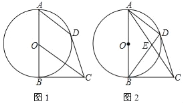
查看答案和解析>>【题目】如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD
(1)求证:CD是⊙O的切线;
(2)如图2,连AC交BD于E.若AE=CE,求tan∠ACB的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别是x轴、y轴上的点,点A的坐标为(a,0),点B的坐标为(0,b),点M坐标为(1,1)
(1)如图1中的第一象限内,若a=2,b=1,画出线段AB关于点M(1,1)的中心对称线段CD,并写出C、D两点的坐标;
(2)如图,若AB关于M(1,1)中心对称的线段为CD,点C、点D在双曲线y=
 (x>0)上,且AB=
(x>0)上,且AB= ,求k的值;
,求k的值;(3)若a=
 ,b=
,b= ,直接写出直线CD的解析式.
,直接写出直线CD的解析式.
相关试题

