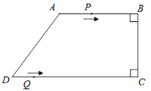
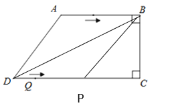
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠BCD=90°,AD=10cm,BC=8cm,CD=16cm.点P从点A出发,以每秒3cm的速度沿折线段AB—BC—CD运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,设运动时间为t秒(![]() ).
).
(1)求AB的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P运动过程中,当![]() 秒的时候,使得△BPD的面积为20cm2.
秒的时候,使得△BPD的面积为20cm2.
参考答案:
【答案】(1)10;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)如图1中,作AH⊥CD于H.则四边形ABCH是矩形解直角三角形求出DH即可解决问题;
(2)当四边形PBQD为平行四边形时,点P在AB上,点Q在DC上,根据PB=DQ构建方程解决问题即可;
(3)分三种情形:①当点P在线段AB上时.②当点P在线段BC上时.③当点P在线段CD上时,分别利用三角形三角形面积公式列方程计算求解即可.
解:(1)如图1中,作AH⊥CD于H.
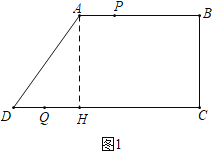
∵∠AHC=∠B=∠C=90°,
∴四边形ABCH是矩形,
∴AH=BC=8cm,AB=CH,
在Rt△ADH中,∵∠AHD=90°,AD=10cm,AH=8cm,
∴DH=![]() (cm),
(cm),
∴AB=CH=CD-DH=16-6=10(cm).
(2)当四边形![]() 为平行四边形时,
为平行四边形时,
![]() 且
且![]() .
.
由题知:BP=10-3t,DQ=2t,
∴![]() ,解得:
,解得:![]()
∴![]() ,
,
∴![]()
∴![]()
![]()
∴平行四边形![]() 的周长
的周长![]() .
.

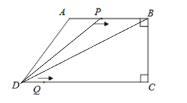
(3)当![]() 在线段
在线段![]() 上时,
上时,![]() ,
,
![]() ,解得
,解得![]()
当![]() 在线段
在线段![]() 上时,
上时,![]() ,
,
![]() ,解得
,解得![]()
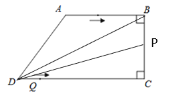
当点![]() 在线段
在线段![]() 上时,DP=34-3t
上时,DP=34-3t
![]() ,解得
,解得![]() (由
(由![]() ,所以此解舍去),
,所以此解舍去),
综上所述,![]() ,或
,或![]() 秒
秒
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法
没有影响
影响不大
影响很大
学生人数(人)
40
60
m

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明袋子中有1个红球和3个白球,这些球除颜色外都相同.
(1)从袋中任意摸出2个球,用树状图或列表求摸出的2个球颜色不同的概率;
(2)在袋子中再放入x个白球后,进行如下实验:从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀.经大量试验,发现摸到白球的频率稳定在0.95左右,求x的值.
-
科目: 来源: 题型:
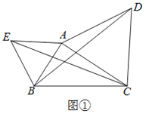
查看答案和解析>>【题目】△ABC中,BC=8,以AC为边向外作等边△ACD.
(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;
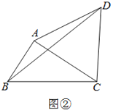
(2)如图②,若∠ABC=60°,AB=4,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据:
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中有正方形AOBC,O为坐标原点,点A、B分别在y轴、x轴正半轴上,点P、E、F分别为边BC、AC、OB上的点,EF⊥OP于M.
(1)如图1,若点E与点A重合,点A坐标为(0,8),OF=3,求P点坐标;
(2)如图2,若点E与点A重合,且P为边BC的中点,求证:CM=2CP;
(3)如图3,若点M为线段OP的中点,连接AB交EF于点N,连接NP,试探究线段OP与NP的数量关系,并证明你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.
(1)按如图所示建立平面直角坐标系,求表示该抛物线的函数表达式;
(2)一辆货运卡车高为4m,宽为2m,如果该隧道内设双向车道,那么这辆货车能否安全通过?

相关试题

