【题目】平面直角坐标系中有正方形AOBC,O为坐标原点,点A、B分别在y轴、x轴正半轴上,点P、E、F分别为边BC、AC、OB上的点,EF⊥OP于M.
(1)如图1,若点E与点A重合,点A坐标为(0,8),OF=3,求P点坐标;
(2)如图2,若点E与点A重合,且P为边BC的中点,求证:CM=2CP;
(3)如图3,若点M为线段OP的中点,连接AB交EF于点N,连接NP,试探究线段OP与NP的数量关系,并证明你的结论.



参考答案:
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ,证明见解析
,证明见解析
【解析】
(1)证明△OAF≌△BOP(ASA),得出OF=PB=3,则P点坐标可求出;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用
,利用![]() ,
,![]() 证得四边形
证得四边形![]() 为平行四边形,然后根据直角三角形斜边中线等于斜边的一半求得MN=AN,用HL定理证明
为平行四边形,然后根据直角三角形斜边中线等于斜边的一半求得MN=AN,用HL定理证明![]() ,从而求得
,从而求得![]() 为
为![]() 的垂直平分线,使问题得解;
的垂直平分线,使问题得解;
(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,由矩形和正方形的性质求得
,由矩形和正方形的性质求得![]() 为等腰直角三角形,从而求得
为等腰直角三角形,从而求得![]() ,
,![]() ,利用垂直平分线的性质求得ON=NP,然后根据HL定理证得
,利用垂直平分线的性质求得ON=NP,然后根据HL定理证得![]() ,然后利用全等三角形的性质求得
,然后利用全等三角形的性质求得![]() ,即
,即![]() 为等腰直角三角形,从而使问题得解.
为等腰直角三角形,从而使问题得解.
解:∵A(0,8),
∴OA=8,
∵EF⊥OP于M,
∴∠OMF=90°,
∴∠MOF+∠OFM=90°,
∵∠OFM+∠OAF=90°,
∴∠MOF=∠OAF.
∵OA=OB,∠AOF=∠OBP,
∴△OAF≌△BOP(ASA),
∴OF=PB=3,
∴P(8,3);

(2)取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
∵在正方形AOBC中,OA=BC=AC,且点P为BC中点
∴![]() ,
,![]()
∴![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∵EF⊥OP
∴![]()
又∵N为OA中点
∴在Rt△AOM中,MN=AN
在Rt△AHN和Rt△MHN中,MN=AN,NH=NH
∴![]()
∴![]() ,
,![]() 为
为![]() 的垂直平分线
的垂直平分线
∴![]()

(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
由题意可知四边形AHGC是矩形且四边形AOBC为正方形
∴HG=AC=OA
在正方形AOBC中,∠OAB=45°
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,![]()
由EF⊥OP于M且M为OP的中点
∴MN垂直平分OP
∴ON=NP
在Rt△ONH和Rt△NPG中![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() .
.

-
科目: 来源: 题型:
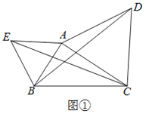
查看答案和解析>>【题目】△ABC中,BC=8,以AC为边向外作等边△ACD.
(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;
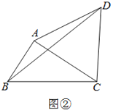
(2)如图②,若∠ABC=60°,AB=4,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠BCD=90°,AD=10cm,BC=8cm,CD=16cm.点P从点A出发,以每秒3cm的速度沿折线段AB—BC—CD运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,设运动时间为t秒(
 ).
).(1)求AB的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P运动过程中,当
 秒的时候,使得△BPD的面积为20cm2.
秒的时候,使得△BPD的面积为20cm2.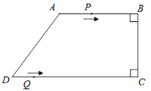
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据:
 ≈1.41,
≈1.41,  ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.
(1)按如图所示建立平面直角坐标系,求表示该抛物线的函数表达式;
(2)一辆货运卡车高为4m,宽为2m,如果该隧道内设双向车道,那么这辆货车能否安全通过?

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN、MN,
(1)求证:△CMN是等边三角形;
(2)判断CN与⊙O的位置关系,并说明理由;
(3)若AD:AB=3:4,BN=4,求等边△ABC的边长.

相关试题

