搜索
【题目】已知：甲、乙两车分别从相距300千米的A，B两地同时出发相向而行，甲到B地后立即返回，下图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．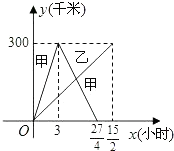
（1）请直接写出甲、乙两车离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数关系式，并标明自变量x的取值范围；
（2）它们在行驶的过程中有几次相遇？并求出每次相遇的时间．
参考答案：
【答案】
（1）解：甲由3小时到 
小时的速度是： 
=80千米/小时．
（2）解：由题意有两次相遇．
方法一：①当0≤x≤3时，100x+40x=300，解得 
，
②当 
时，（540﹣80x）+40x=300，解得x=6，
综上所述，两车第一次相遇时间为第 
小时，第二次相遇时间为第6小时．
方法二：设经过x小时两车首次相遇，
则40x+100x=300，解得 ，
设经过x小时两车第二次相遇，
则80（x﹣3）=40x，解得x=6．
综上所述，两车第一次相遇时间为第 小时，第二次相遇时间为第6小时．
【解析】（1）依图可知甲的图像是折线，y甲的函数关系式为分段函数，乙是线段；（2）根据第一次相遇时二者的路程和=300可列出方程100x+40x=300，第二次是甲追上乙，利用甲余下的路程加乙的路程和=300即（540﹣80x）+40x=300，解出方程即可解出.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，∠BAC=120°，S△ABC=8
，点M，P，N分别是边AB，BC，AC上任意一点，则：（1）AB的长为____________．
（2）PM+PN的最小值为____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了响应“足球进校园”的目标，某校计划为学校足球队购买一批足球，已知购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元．
（1）求A，B两种品牌的足球的单价．
（2）该校打算通过“京东商城”网购20个A品牌的足球和3个B品牌的足球，“五一”期间商城打折促销，其中A品牌打八折，B品牌打九折，问：学校购买打折后的足球所花的费用比打折前节省了多少钱？
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题情境：如图1，AB∥CD，∠PAB=135°，∠PCD=125°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可求得∠APC的度数．请写出具体求解过程．
问题迁移：
(1)如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=∠α，∠BCP=∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；
(2)在(1)的条件下，如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)，请你直接写出∠CPD、∠α、∠β间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为选拔参加八年级数学“拓展性课程”活动人选，数学李老师对本班甲、乙两名学生以前经历的10次测验成绩（分）进行了整理、分析（见图①）：
（1）写出a，b的值；
（2）如要推选1名学生参加，你推荐谁？请说明你推荐的理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在菱形ABCD中，∠ABC=60°，E是对角线AC上一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF．
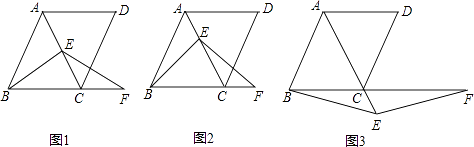
（1）若E是线段AC的中点，如图1，易证：BE=EF（不需证明）；
（2）若E是线段AC或AC延长线上的任意一点，其它条件不变，如图2、图3，线段BE、EF有怎样的数量关系，直接写出你的猜想；并选择一种情况给予证明． -
科目： 来源： 题型：
查看答案和解析>>【题目】数学活动课上，老师准备了若干个如图1的三种纸片，
种纸片是边长为
的正方形，
种纸片是边长为
的正方形，
种纸片是长为，宽为的长方形.并用种纸片一张，种纸片一张，种纸片两张拼成如图2的大正方形．
（1）请用两种不同的方法求图2大正方形的面积：方法1：_______；方法2：________；
（2）观察图2，请你写出代数式：
之间的等量关系________；（3）根据（2）题中的等量关系，解决如下问题：
①已知：
，求
的值；②已知
，求
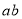的值；③已知(a-2019)2+(a-2021)2=8，则求(a-2020)2的值．
相关试题
