【题目】数学活动课上,老师准备了若干个如图1的三种纸片,![]() 种纸片是边长为
种纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片是边长为
种纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片是长为
种纸片是长为![]() ,宽为
,宽为![]() 的长方形.并用
的长方形.并用![]() 种纸片一张,
种纸片一张,![]() 种纸片一张,
种纸片一张,![]() 种纸片两张拼成如图2的大正方形.
种纸片两张拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积:方法1:_______;方法2:________;
(2)观察图2,请你写出代数式:![]() 之间的等量关系________;
之间的等量关系________;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值;
的值;
③已知(a-2019)2+(a-2021)2=8,则求(a-2020)2的值.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() ;③
;③![]()
【解析】
(1)方法1:图2是边长为![]() 的正方形,利用正方形的面积公式可得出
的正方形,利用正方形的面积公式可得出![]() ;方法2:图2可看成1个边长为
;方法2:图2可看成1个边长为![]() 的正方形、1个边长为
的正方形、1个边长为![]() 的正方形以及2个长为
的正方形以及2个长为![]() 宽为
宽为![]() 的长方形的组合体,根据正方形及长方形的面积公式可得出
的长方形的组合体,根据正方形及长方形的面积公式可得出![]() ;
;
(2)由图2中的图形面积不变,可得出![]() =
=![]() ;
;
(3)①由![]() 可得出
可得出![]() =25,将其和
=25,将其和![]() 代入
代入![]() =
=![]() 中即可求出
中即可求出![]() 的值;
的值;
②设![]() ,
,![]() ,则
,则![]() ,由已知得出
,由已知得出![]() ,代入
,代入![]() 中即可求出
中即可求出![]() 的值,即可求解;
的值,即可求解;
③设![]() ,则
,则![]() ,
,![]() ,通过整理可求得
,通过整理可求得![]() ,即可求解.
,即可求解.
(1)方法1:图2是边长为![]() 的正方形,
的正方形,
∴![]() ;
;
方法2:图2可看成1个边长为![]() 的正方形、1个边长为
的正方形、1个边长为![]() 的正方形以及2个长为
的正方形以及2个长为![]() 宽为
宽为![]() 的长方形的组合体,
的长方形的组合体,
∴![]() .
.
故答案为:![]() ;
;![]() ;
;
(2)由(1)可得:![]() =
=![]() .
.
故答案为:![]() ;
;
(3)①∵![]() ,
,
∴![]() =25,
=25,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
②设![]() ,
,![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]()
即![]() ;
;
③设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,即
,即![]() ,
,
整理得:![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:甲、乙两车分别从相距300千米的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
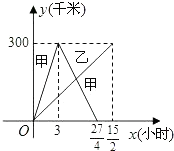
(1)请直接写出甲、乙两车离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并标明自变量x的取值范围;
(2)它们在行驶的过程中有几次相遇?并求出每次相遇的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】为选拔参加八年级数学“拓展性课程”活动人选,数学李老师对本班甲、乙两名学生以前经历的10次测验成绩(分)进行了整理、分析(见图①):

(1)写出a,b的值;
(2)如要推选1名学生参加,你推荐谁?请说明你推荐的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
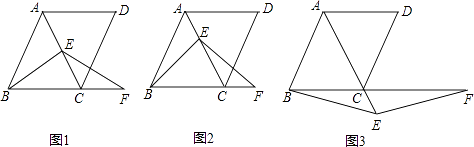
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为
 ,
, ,
, ,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形
,把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形 .
. (1)画出三角形ABC和平移后
 的图形;
的图形;(2)写出三个顶点
 ,
, ,
, 的坐标;
的坐标;(3)求三角形ABC的面积.

相关试题

