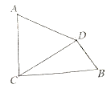
【题目】如图,AC⊥BC,垂足为C,AC=6,BC=4![]() ,将线段AC绕点C按顺时针方向旋转60°,得到线段CD,连接AD,DB。
,将线段AC绕点C按顺时针方向旋转60°,得到线段CD,连接AD,DB。
(1)求线段BD的长度;
(2)求四边形ACBD的面积.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]()
![]() .
.
【解析】
(1)由旋转可得△ACD是等边三角形,过点D作DE⊥BC于点E,在Rt△CDE中,分别求得DE,CE的长,再由勾股定理在Rt△ BDE中求得BD的长.(2)四边形ACBD的面积可分为梯形ACED和三角形DEB的面积.
解:
(1)由旋转得AC=CD=6,∠ACD=60°,
∴△ACD是等边三角形,
过点D作DE⊥BC于点E,
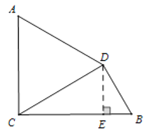
∵AC⊥BC,
∴∠DCE=∠ACB-∠ACD=90°-60°=30°
∴在Rt△CDE中,
![]() ,
,
![]() ,
,
∴ ![]() .
.
∴ Rt△ BDE中,
![]() .
.
(2)S四边形ACBD= S梯形ACED+ S△EBD,
=![]() ,
,
=![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,
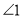 与
与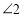 是直线________和________被直线________所截得的________角.
是直线________和________被直线________所截得的________角.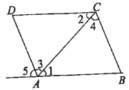
(2)
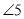 与
与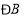 是直线________和________被直线________所截得的________角.
是直线________和________被直线________所截得的________角.(3)
 与
与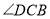 是直线________和________被直线________所截得的________角.
是直线________和________被直线________所截得的________角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图是一个跳棋棋盘,其游戏规则是一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上例如:从起始位置
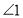 跳到终点位置
跳到终点位置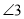 有两种不同路径,路径1:
有两种不同路径,路径1: ;路径2:
;路径2: .
.
试一试:(1)写出从起始位置
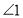 跳到终点位置
跳到终点位置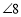 的一种路径;
的一种路径;(2)从起始位置
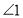 依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置
依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点位置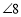 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织初一师生春游,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车,可少租1辆,且余15个座位.
(1)求参加春游的人数;
(2)已知租用45座的客车日租金为每辆车250元, 60座的客车日租金为每辆300元,问租哪种客车更合算?省多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E。
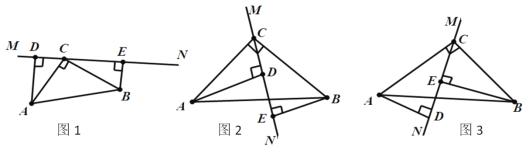
(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你写出这个数量关系,并证明
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣ x2+bx+c经过点A,B.
x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

-
科目: 来源: 题型:
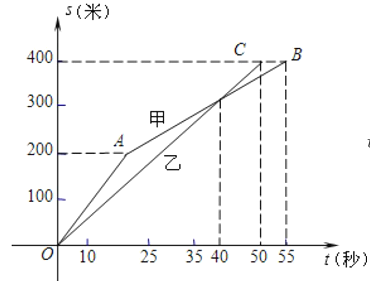
查看答案和解析>>【题目】如图,在甲、乙两名同学进行400米跑步比赛中,路程S(米)与时间(t)之间的函数关系的图像分别为折线OAB和线段OC请根据图上信息回答下列问题
(1) 先到达终点;
(2)第 秒时, 追上 ;
(3)比赛过程中, 的速度适中保持不变;
(4)优胜者在比赛过程中所跑的路程S(米)关于时间t(秒)的函数解析式及定义域为 .
相关试题

