【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
参考答案:
【答案】(1)证明见试题解析;(2)20.
【解析】
试题(1)先证∠BAE=∠BCF,又由BA=BC,AE=CF,得到△BAE≌△BCF;
(2)由已知可得四边形BFDE对角线互相垂直平分,只要∠EBF=90°即得四边形BFDE是正方形,由△BAE≌△BCF可知∠EBA=∠FBC,又由∠ABC=50°,可得∠EBA+∠FBC=40°,于是∠EBA=![]() ×40°=20°.
×40°=20°.
试题解析:(1)∵菱形ABCD的对角线AC,BD相交于点O,∴AB=BC,∠BAC=∠BCA,∴∠BAE=∠BCF,在△BAE与△BCF中,∵BA=BC,∠BAE=∠BCF,AE=CF,∴△BAE≌△BCF(SAS);
(2)∵四边形BFDE对角线互相垂直平分,∴只要∠EBF=90°即得四边形BFDE是正方形,∵△BAE≌△BCF,∴∠EBA=∠FBC,又∵∠ABC=50°,∴∠EBA+∠FBC=40°,∴∠EBA=![]() ×40°=20°.故答案为:20.
×40°=20°.故答案为:20.
-
科目: 来源: 题型:
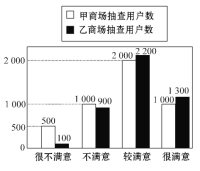
查看答案和解析>>【题目】在“3·15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分.
(1)分别求出甲、乙两商场的用户满意度分数的平均值(计算结果精确到0.01).
(2)请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C是线段AB上的一点,点D是线段AB的中点,点E是线段BC的中点.
(1)当AC=8,BC=6时,求线段DE的长度;
(2)当AC=m,BC=n(m>n)时,求线段DE的长度;
(3)从(1)(2)的结果中,你发现了什么规律?请直接写出来.
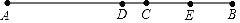
-
科目: 来源: 题型:
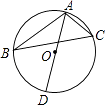
查看答案和解析>>【题目】如图,△ABC的三个顶点都在⊙O上,AD是直径,且∠CAD=56°,则∠B的度数为( )
A.44°
B.34°
C.46°
D.56° -
科目: 来源: 题型:
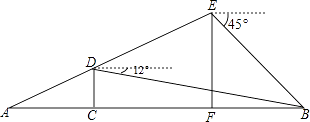
查看答案和解析>>【题目】“星光隧道”是贯穿新牌坊商圈和照母山以北的高端居住区的重要纽带,预计2017年底竣工通车,图中线段AB表示该工程的部分隧道,无人勘测飞机从隧道一侧的点A出发,沿着坡度为1:2的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为12°,继续飞行到点E,测得点B的俯角为45°,此时点E离地面高度EF=700米,则隧道BC段的长度约为( )米.(参考数据:tan12°≈0.2,cos12°≈0.98)
A.2100
B.1600
C.1500
D.1540 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师给出了如下问题:如图,∠AOB=80°,OC平分∠AOB,若∠BOD=20°.
(1)请你补全图形,并求∠COD的度数;
(2)若∠BOD=
 其他条件不变,请直接写出∠COD的度数.
其他条件不变,请直接写出∠COD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数a使关于x的不等式组
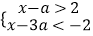 无解,且使关于x的分式方程
无解,且使关于x的分式方程 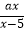 ﹣
﹣ 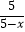 =﹣3有正整数解,则满足条件的a的值之积为( )
=﹣3有正整数解,则满足条件的a的值之积为( )
A.28
B.﹣4
C.4
D.﹣2
相关试题

