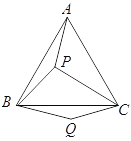
【题目】如图, ![]() 是等边三角形
是等边三角形![]() 内的一点,连结
内的一点,连结![]() 、
、![]() 、
、![]() ,以
,以![]() 为边作
为边作![]() 且
且![]() .连结
.连结![]() .
.
(1)观察并猜想![]() 与
与![]() 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.
(2)若![]() ,
, ![]() ,
, ![]() ,连结
,连结![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)在(2)的条件下,求![]() 的面积.
的面积.
参考答案:
【答案】(![]() )
)![]() ,证明见解析;(
,证明见解析;(![]() )
)![]() 为直角三角形,理由见解析;(
为直角三角形,理由见解析;(![]() )
)![]() .
.
【解析】试题分析:(1)通过证明△ABP≌△CBQ得出;(2)根据△BPQ是等边三角形求出PQ的长,再根据勾股定理逆定理可得△PQC是直角三角形;(3)过点B作BD垂直于CQ的延长线于点D,在△BDQ中求出DQ、BD的长,再求出CD,根据勾股定理求出BC的长,即可求出三角形ABC面积.
解:(1)AP=CQ,
理由:∵∠PBQ=60°,∠ABC=60°,
∴∠ABP+∠PBC=60°=∠CBQ+∠PBC,
∴∠ABP=∠CBQ,
在△ABP与△CBQ中,AB=CB,∠ABP=∠CBQ,BP=BQ,
∴△ABP≌△CBQ,
∴AP=CQ.
(2)∵BP=BQ,∠PBQ=60°,
∴△BPQ为等边三角形,
∴PQ=PB=4,
∵△ABP≌△CBQ,∴AP=CQ=3,
∵PQ2+CQ2=42+32=25=PC2,
∴△PQC为直角三角形.
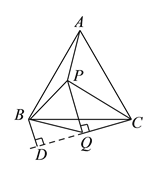
(3)∵∠PQC=90°,∠PQB=60°,
∴∠BQC=150°,
过点B作BD垂直于CQ的延长线于点D,
∴∠BQD=30°,
∵BQ=4,∴BD=2,DQ=2![]() ,
,
∴CD=CQ+DQ=3+![]() ,
,
在Rt△BCD中,BC=![]() ,
,
∵△ABC为等边三角形,
∴S△ABC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形的面积为4a2-4b2,如果它的一边长为a+b,则它的周长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在AQ(弧)上且不与A点重合,但Q点可与B点重合.
发现.AP(弧)的长与QB(弧)的长之和为定值l,求l;
思考.点M与AB的最大距离为_______,此时点P,A间的距离为_______;点M与AB的最小距离为________,此时半圆M的弧与AB所围成的封闭图形面积为________.
探究.当半圆M与AB相切于T时,求AT的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为
 的正方形
的正方形 中,点
中,点 在
在 上从
上从 向
向 运动,连接
运动,连接 交
交 于点
于点 .
.(
 )试证明:无论点
)试证明:无论点 运动到
运动到 上何处时,都有
上何处时,都有 ≌
≌ .
.(
 )若点
)若点 从点
从点 运动到点
运动到点 ,再继续在
,再继续在 上运动到点
上运动到点 ,在整个运动过程中,点
,在整个运动过程中,点 以每秒
以每秒 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当 恰为等腰三角形,求点
恰为等腰三角形,求点 运动的时间.
运动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(x4)3+(x3)4﹣2x4x8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】把角度化为度、分的形式,则20.5°=20°′.
相关试题

