搜索
【题目】如图，隧道的截面由抛物线和长方形构成，长方形的长是8m，宽是2m，抛物线的最高点到路面的距离为6米．
（1）按如图所示建立平面直角坐标系，求表示该抛物线的函数表达式；
（2）一辆货运卡车高为4m，宽为2m，如果该隧道内设双向车道，那么这辆货车能否安全通过？
参考答案：
【答案】
（1）解：如图1，
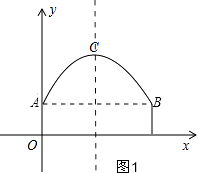
由题意得：最高点C（4，6），B（8，2），
设抛物线的函数表达式：y=a（x﹣4）2+6，
把（8，2）代入得：a（8﹣4）2+6=2，
a=﹣ 
，
∴y=﹣ （x﹣4）2+6
（2）解：如图2，
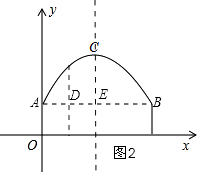
当DE=2时，
AD=AE﹣DE=4﹣2=2，
当x=2时，y=﹣ （2﹣4）2+6=5＞4，
∴这辆货车能安全通过．
【解析】（1）由题意得出B、C两点的坐标，设出抛物线的顶点式，用待定系数法即可求解；（2）货车外侧与地面接触点的横坐标为2，将X=2带入抛物线的解析式求出对应的Y值，再将此值与4比大小即可。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E．
（1）证明：四边形ACDE是平行四边形；
（2）若AC=8，BD=6，求△ADE的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，物理实验室有一单摆在左右摆动，摆动过程中选取了两个瞬时状态，从C处测得E，F两点的俯角分别为∠ACE=60°，∠BCF=45°，这时点F相对于点E升高了4cm．求该摆绳CD的长度．（精确到0.1cm，参考数据：
≈1.41， 
≈1.73）
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明：
如图，BE平分∠ABD，DE平分∠BDC，且∠α+∠β=90°，求证：AB∥CD．
证明：∵BE平分∠ABD(已知)，∴∠ABD=2∠α( )
∵DE平分∠BDC( )
∴∠BDC= ( )，∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换)
∵∠α+∠β=90°(已知)，∴∠ABD+∠BDC=( )，∴AB∥CD( )
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形
中，
，
，
．
（1）求证：
；（2）若
，
，
，
分别是
，
，
，
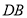的中点，求证：线段
与线段
互相平分． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB，CD相交于点O，OM⊥AB．
（1）∠AOC的邻补角为 （写出一个即可）；
（2）若∠1=∠2，判断ON与CD的位置关系，并说明理由；
（3）若∠1=
∠BOC，求∠MOD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，将两个边长为1的小正方形分别沿对角线剪开，拼成正方形ABCD．
（1）正方形ABCD的面积为 ，边长为 ，对角线BD= ；
（2）求证：
；（3）如图②，将正方形ABCD放在数轴上，使点B与原点O重合，边AB落在x轴的负半轴上，则点A所表示的数为 ，若点E所表示的数为整数，则点E所表示的数为 ．
相关试题
