【题目】如图,Rt△ABO的顶点A是反比例函数y=![]() 与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=
与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=![]() .
.
(1)直接写出这两个函数的关系式;
(2)求△AOC的面积;
(3)根据图象直接写出:当x为何值时,反比例函数的值小于一次函数的值.

参考答案:
【答案】(1)y=![]() ;y=﹣x+2;(2)4;(3)x<﹣1或0<x<3时;
;y=﹣x+2;(2)4;(3)x<﹣1或0<x<3时;
【解析】
(1)先根据反比例函数的图象所在的象限判断出k的符号,在由△ABO的面积求出k的值,进而可得出两个函数的解析式;
(2)把两函数的解析式组成方程组,求出x、y的值,即可得出A、C两点的坐标,再由一次函数的解析式求出直线与x轴的交点,由S△AOC=S△AOD+S△COD进行解答即可.
(3)直接根据一次函数与反比例函数的交点坐标求出一次函数的值大于反比例函数的值x的取值范围即可.
解:(1)设点A(x,y),则xy=k
∵S△AOB=![]()
∴![]() (﹣x)×y=
(﹣x)×y=![]()
∴k=﹣3
∴反比例函数解析式y=![]()
一次函数解析式y=﹣x+2
(2)由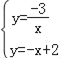
解得![]() ,
,![]()
∴A(﹣1,3)、C(3,﹣1)
∵一次函数y=﹣x+2与y轴的交点坐标为(0,2)
∴S△AOC=![]() ×2×(3+1)=4
×2×(3+1)=4
(3)由图象可得:当x<﹣1或0<x<3时,一次函数图象在反比例图象的上方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答下列各题
(1)解方程:﹣x2+4x﹣3=0.
(2)已知一次函数y=kx+b的图象与反比例函数y=
 的图象交于点A(2,m),B(﹣1、n),求一次函数的解析式.
的图象交于点A(2,m),B(﹣1、n),求一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC,AB=AC,AC的垂直平分线与AB所在直线相交所得的锐角为40°,∠C=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=
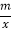 的图象交于A(2,3),B(6,n)两点.
的图象交于A(2,3),B(6,n)两点.(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣x2+1的图象与x轴交于A、B两点,与y轴交于点C,下列说法错误的是( ).
A. 点C的坐标是(0,1) B. 线段AB的长为2
C. △ABC是等腰直角三角形 D. 当x>0时,y随x增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,点 D,E 分别在∠ABC 和∠ACB 的平分线上,连接 BD,DE,EC,若∠D+∠E=295°, 则∠A 是( )
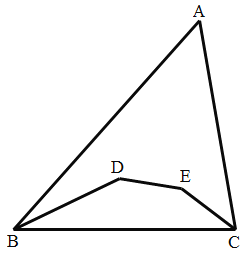
A.65°B.60°C.55°D.50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 和直线
和直线 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .
其中正确的有

A.1个 B.2个 C. 3个 D.4个
相关试题

