Question

【题目】△ABC，AB=AC，AC的垂直平分线与AB所在直线相交所得的锐角为40°，∠C=______.

Answer 1

【答案】65°或25°

【解析】

当△ABC为锐角三角形时，设AC的垂直平分线交线段AB于点D，交AC于点E，在Rt△ADE中可求得∠A，再由三角形内角和定理可求得∠C；当△ABC为钝角三角形时，设AC的垂直平分线交AC于点E，交直线AB于点D，则可求得△CAB的外角，再利用外角的性质可求得∠C，可求得答案．

解：当△ACB为锐角三角形时，如图1，设AC的垂直平分线交线段AB于点D，交AC于点E，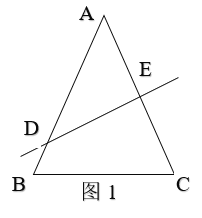

∵∠ADE=40°，DE⊥AC，
∴∠A=90°-40°=50°，
∵AC=AB，
∴∠C=（180°-∠A）=65°；
当△ABC为钝角三角形时，如图2，设AC的垂直平分线交AC于点E，交AB于点D，

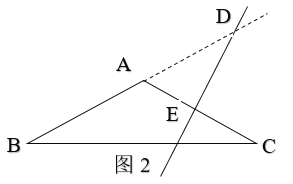
∵∠ADE=40°，DE⊥AC，
∴∠DAC=50°，
∵AC=AB，
∴∠C=∠B，
∵∠C+∠B=∠DAC，
∴∠C=25°；
故答案为： 65°或25°，